Skip to contents

Systematic exploration of the BLV solution space

Source: vignettes/grid.Rmd
grid.Rmd
library(blvim)
## we use ggplot2 for graphical representations
library(ggplot2)

One of the main objectives of the blvim package is to ease the systematic exploration of the BLV model’s solution space when \(\alpha\) and \(\beta\) vary. This is supported by a collection of grid_* functions.

Locations and setup

We shall work with a regular grid of locations, in a symmetric (non-bipartite) case.

locations <- expand.grid(x = 1:5, y = 1:5)
locations$name <- LETTERS[1:25]
ggplot(locations, aes(x, y, label = name)) +
  geom_text() +
  coord_fixed()

A five by five grid showing the regularity of the location positions.

We use the Euclidean distance between the points as the interaction costs.

costs <- as.matrix(dist(locations[c("x", "y")]))

And finally, we consider unitary productions and initial attractivenesses.

location_prod <- rep(1, nrow(locations))
location_att <- rep(1, nrow(locations))

Computing a collection of models

The main function for systematic exploration is grid_blvim(), which computes a collection of spatial interaction models (the BLV models obtained by blvim()) for all pairwise combinations of \(\alpha\) and \(\beta\) provided.

For the \(\alpha\) parameter, we generally recommend focussing on values strictly larger than 1 (setting \(\alpha=1\) significantly slows down the convergence of the fixed-point algorithm used in the BLV model). For \(\beta\), we aim to cover local models (with a large \(\beta\)) and long-range ones (with a small \(\beta\)). Here, distances between positions range from 1 to approximately 7, so a typical range for \(\frac{1}{\beta}\) could be \([0.5 ; 4]\).

The collection of models is computed by grid_blvim() as follows. Note that while we could specify the location data as parameters of the call, it is generally simpler to do so on the resulting sim_list().

models <- grid_blvim(costs,
  location_prod,
  alphas = seq(1.05, 2, length.out = 25),
  betas = 1 / seq(0.5, 4, length.out = 25),
  location_att,
  bipartite = FALSE,
  epsilon = 0.1,
  iter_max = 5000,
  conv_check = 10
)

We specify now the location data.

destination_names(models) <- locations$name
destination_positions(models) <- as.matrix(locations[c("x", "y")])

An important point to note is that the sim_list() returned by grid_blvim() is homogeneous: it uses the same cost matrix and the same location data. This is enforced in the package because most of the exploration methods proposed would not make sense for a heterogeneous collection of spatial interaction models.

Exploring the results

Single model extraction

The sim_list() object behaves like a read-only list. We can therefore extract any of the models, for instance to display the corresponding flows, as demonstrated below for the first model, using both the standard matrix display and the position-based one.

autoplot(models[[1]]) +
  scale_fill_gradient(low = "white", high = "black") +
  coord_fixed()

A matrix representation of the flows. The flows are highly structured with a dominant diagonal (showing strong self interactions) and some diagonal bands. These bands show that most of the flows are local.

autoplot(models[[10]],
  flows = "full", with_positions = TRUE,
  arrow = arrow(length = unit(0.01, "npc"))
) +
  coord_fixed() +
  scale_linewidth_continuous(range = c(0, 1))

A dot and arrow representation of the flows on the five by five regular grid of the locations. This representation show a different type of flow organisation. Locations on the border of the grid (top and bottom rows, leftmost and rightmost columns) concentrate their flows on the internal three by three subgrid.

Variability plot

The sim_list object has a ggplot2::autoplot() function that provides a variability plot. The aim is to display statistics of the flows over the collection of spatial interaction models in the list. The default representation focuses on individual flows as shown below.

autoplot(models, with_names = TRUE) +
  theme_light()

A variability plot displaying flow statistics between geographic locations labeled A through Y on both the x-axis (destination) and y-axis (origin). The plot is a grid where the size and thickness of squares represent the median of flows across various spatial interaction models, as well as other quantiles. The most striking feature is column M, which contains a continuous vertical line of large, thick-bordered squares for every origin, representing the median flow received by the center point (M) from all other locations. Other destination columns, specifically G, I, Q, and S, contain squares of varying sizes and thicknesses, indicating diverse flow levels from specific origins. The majority of the grid is empty, particularly columns A–F, H, J–L, N–P, R, and T–Y, illustrating that many locations receive no incoming flow across any of the models in the collection.

For instance, the M column shows the flows received from all locations by location M (the centre point of the locations). The thick squares correspond to the median of the flow received by M over all the models. The figure shows in particular that many of the locations do not receive incoming flow in any model.

The position-based figure shows only the destination flows, using circles to display statistics of those flows.

autoplot(models, flows = "destination", with_positions = TRUE) +
  scale_size_continuous(range = c(0, 7)) +
  coord_fixed()

A position-based variability plot showing destination flows across a 5x5 coordinate grid. The x and y axes represent spatial coordinates. Five locations are plotted: a central point at (3, 3) representing location M, and four surrounding points at (2, 2), (2, 4), (4, 2), and (4, 4). The central location (M) features a significantly larger, thick-bordered circle, indicating a high median flow compared to other locations. A tiny dot is visible at the very center of this circle, representing the 0.05 quartile and indicating that in a small fraction of the models, this location receives almost no flow. The four surrounding locations are represented by smaller circles with central dots. The edges of the grid (coordinates 1 and 5) are empty, confirming that the external locations receive no incoming flow in any of the models.

The figure confirms that the external locations receive no flow. The median flow received by M, the central location, is significantly larger than other flows. The tiny internal circle for this location shows the 0.05 quartile: this indicates that for a few models in the list, the central location does not receive any flow. This is illustrated for the first model of the list in the figure above.

Statistics-oriented display

In addition to the variability of the flows, we can display a numerical value for each spatial interaction model on a single plot. To facilitate this, the collection of models first has to be integrated into a data frame-like model. This is done with the sim_df() function.

models_df <- sim_df(models)

The result is a data frame with a special sim column that contains the original sim_list() object as well as the parameters used to build the model (\(\alpha\) and \(\beta\)), diagnostics on the blvim() runs, and the Shannon diversity() of the models.

knitr::kable(head(models_df))
alpha beta diversity iterations converged sim
1.050000 2 24.885897 640 TRUE c(0.6908….
1.089583 2 24.844876 910 TRUE c(0.6890….
1.129167 2 24.758832 2040 TRUE c(0.6875….
1.168750 2 23.174828 5001 FALSE c(0.6796….
1.208333 2 8.776566 2640 TRUE c(0.7026….
1.247917 2 5.770688 1160 TRUE c(0.5686….

The sim_df() object has a ggplot2::autoplot() function which shows by default the diversities of the models.

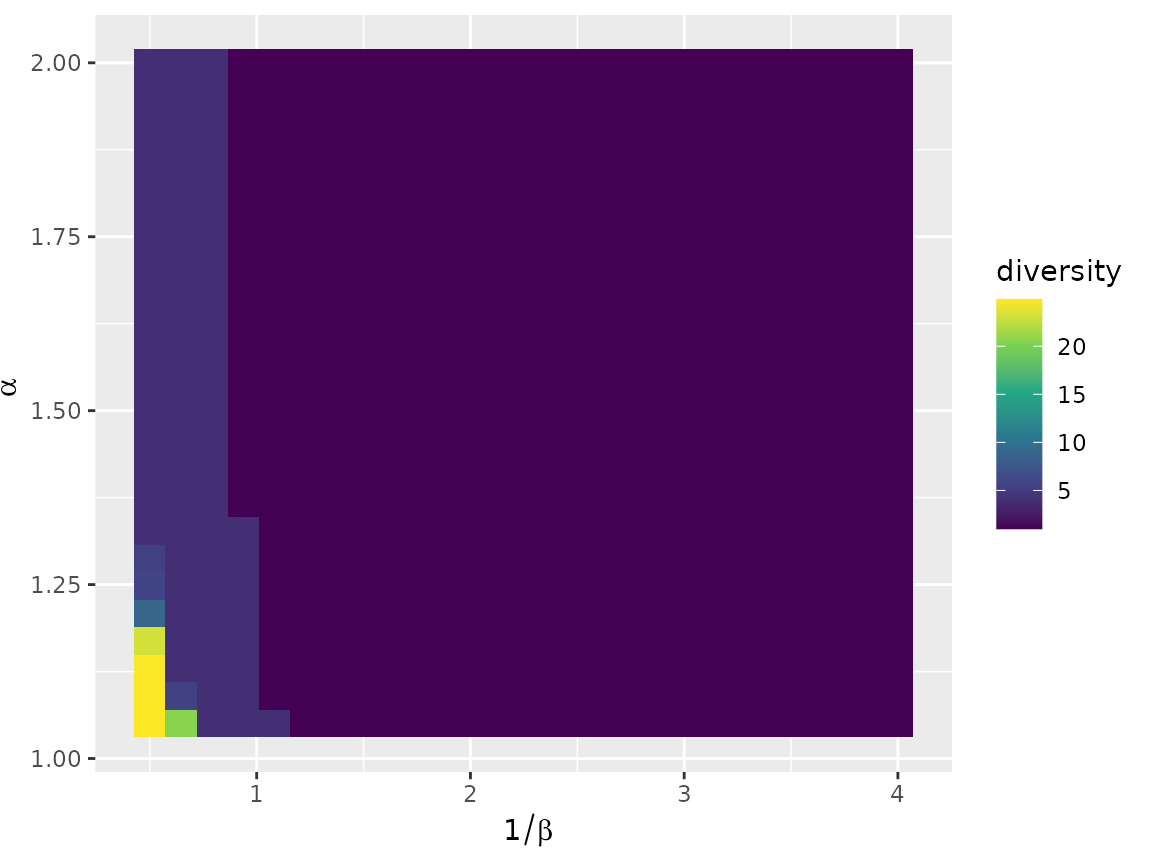
A heatmap plot showing the diversity of incoming flows relative to two model parameters: alpha (return to scale) on the y-axis (ranging from 1.05 to 2.00) and one over beta (cost scale) on the x-axis (ranging from 0.5 to 4.0). Diversity values are represented by a color gradient, where dark purple indicates low diversity (around 5) and bright yellow indicates high diversity (up to almost 25). The plot reveals that high diversity is concentrated in a very specific region: the bottom-left corner, where both alpha is low (near 1.0) and 1 over beta is low (below 1.0). As either α or 1/β increases, the diversity drops sharply. The vast majority of the parameter space - specifically when 1/β is greater than 1.2 or α is greater than 1.3 - is a uniform dark purple, indicating that flow diversity remains consistently low for most parameter combinations.

The figure shows, for each combination of parameters \(\alpha\) and \(\beta\), a coloured rectangle that represents the chosen numerical value for the corresponding model. One can display any column of the sim_df object, for instance the convergence status.

autoplot(models_df, converged)

This heatmap, organized identically to the previous figure showing diversity, displays the convergence status of the models across the α and 1/β parameter space. The vast majority of the plot is cyan, indicating that the models converged (TRUE). Only two small squares in the bottom-left corner are salmon-colored, indicating non-convergence (FALSE) at very low values of both parameters.

The autoplot.sim_df() function uses tidy evaluation, which enables the user to compute interesting values on the fly, as in the following figure that displays the number of terminals per model, according to the Nystuen and Dacey definition.

autoplot(models_df, diversity(sim, "ND")) +
  scale_fill_viridis_c()

A heatmap nearly identical in structure to the previous diversity figure, but calculated using the Nystuen and Dacey definition. It maps diversity values across the same parameter space (α on the y-axis and 1/β on the x-axis). The visual pattern remains consistent: high diversity (yellow) is restricted to the bottom-left corner where both parameters are low, while the rest of the parameter space shows uniform low diversity (dark purple). The main difference is that the ND diversities are integers, but that does not appear on the graphical representation.

Organising the results

Clustering the models

The set of all models, while structured, can be difficult to understand completely using only the tools presented above. To take the analysis further, it may be useful to cluster the models and to display representative elements of the clusters. To ease this task, we support distance-based approaches (such as hierarchical clustering and partitioning around medoids) via sim_distance(). For instance, the following call computes all pairwise Euclidean distances between the destination flows of the models in a sim_list().

models_dist <- sim_distance(models, "destination")

This can then be used as the input of a hierarchical clustering.

models_hc <- hclust(models_dist, method = "ward.D2")

For the studied example, the structure of the model set is highly specific, as a very large subset of them is the same model, with all the flow sent to the central location. This is partly visible in the dendrogram of the clustering, with the large cluster on the left.

plot(models_hc, hang = -1, labels = FALSE)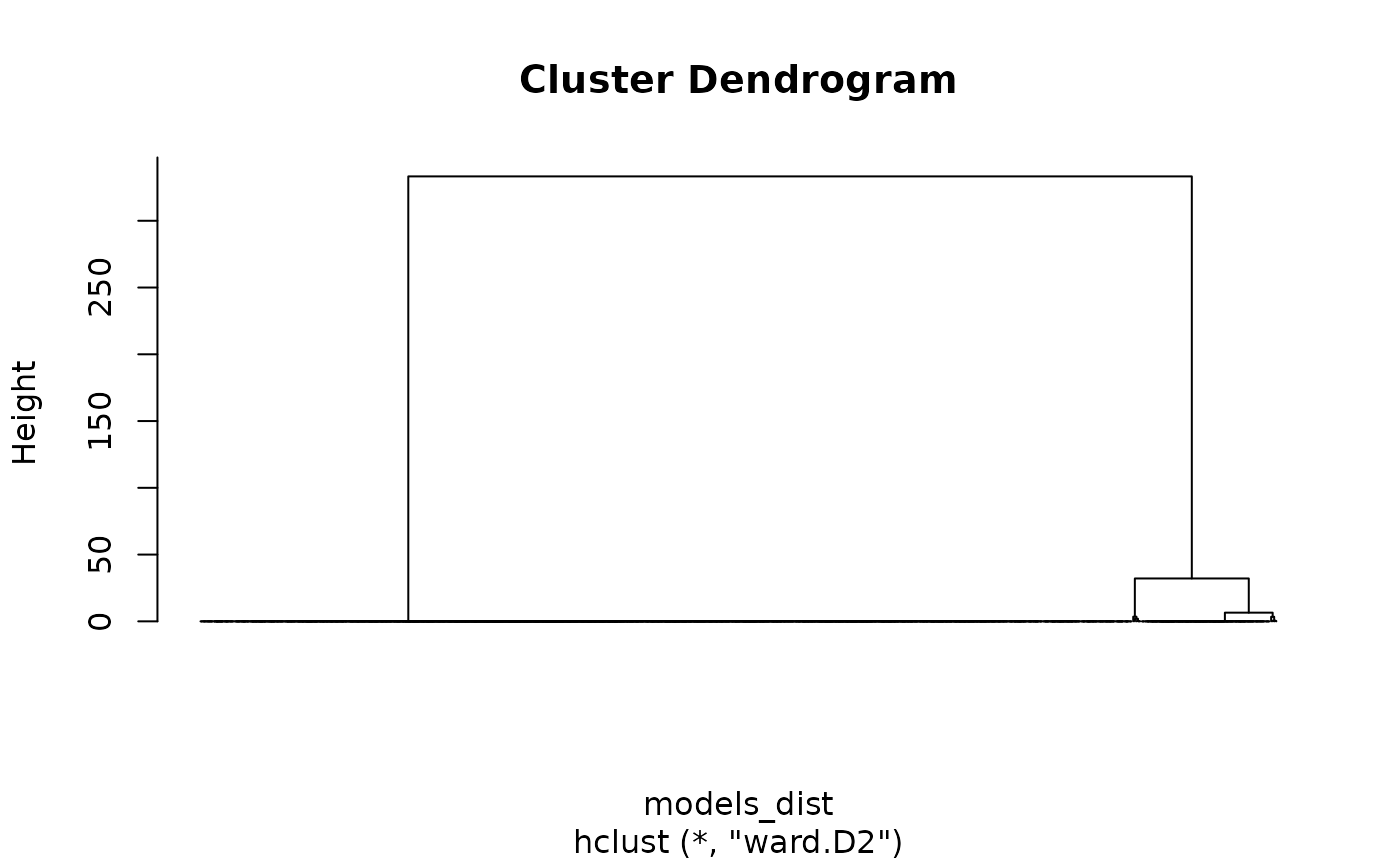

A Cluster Dendrogram showing hierarchical clustering of the models using the ward.D2 method. The y-axis, labeled Height, indicates the distance between clusters. The plot reveals two primary, distinct branches that join at a high level (above 300). The branch on the left consists of a very large group of models with near-zero distance between them, while the smaller branch on the right shows more internal variation with sub-clusters joining at heights between 0 and 50.

Since we use clustering primarily to explore the result set, we can set the number of clusters to an arbitrary value: we are not looking for a clustering structure but rather we want to summarise the model set. A small number of clusters will generally provide a summary that is too crude, while a large number will be difficult to analyse. Here, we arbitrarily chose 16 clusters.

The best way to integrate the clustering result for further analysis is to add a new column to the sim_df() giving the class membership, as follows for instance:

models_df$cluster <- as.factor(cutree(models_hc, k = 16))

This can be immediately used in the standard sim_df() visualisation.

autoplot(models_df, cluster)

A heatmap visualizing the distribution of 16 clusters resulting from hierarchical clustering across the parameter space defined by α on the y-axis (ranging from 1.00 to 2.00) and 1/β on the x-axis (ranging from 0.5 to 4.0). Each distinct color corresponds to one of the 16 numerical clusters shown in the legend. The majority of the parameter space, specifically regions with higher α or 1/β values, is dominated by a single large purple region (cluster 13). A distinct teal vertical band (cluster 7) occupies the left side where 1/β is low. The bottom-left corner and the bottom edge, representing low values for both parameters, are highly fragmented into many small, distinct colored blocks representing the remaining diverse clusters.

Showing cluster variability

Two functions are available in blvim to leverage any partition of a collection of spatial interaction models. Both of them use ggplot2::facet_wrap() to combine standard individual visualisations into an organised one. The first function, grid_var_autoplot(), shows a variability representation for each of the groups identified by a partitioning variable in a sim_df() object.

Using the clustering obtained above, we simply execute:

grid_var_autoplot(models_df, cluster)

A 4x4 grid of 16 variability plots, each labeled 1 through 16, representing clusters of spatial interaction models. Each subplot is a matrix grid showing statistics on the flow from origin (y-axis) to destination (x-axis). There are four model classes: Central Dominance (clusters 13-16) showing heavy flow to the center; Dominant Diagonal (clusters 1-3) indicating self-interaction; No Central Flow (clusters 4 and 9) where the center location receives nothing; and Complex Patterns (clusters 5-8 and 10-12) showing flows to multiple regional hubs. The visual redundancy between many subplots (especially 13-16) suggests that the models within these groups are nearly identical despite being assigned to separate clusters.

This gives a flow variation panel for each of the 16 clusters. The redundancy in the display suggests that we requested too many clusters, but apart from that, the representation outlines a collection of very distinct model classes:

  • a model of central dominance (clusters 13 to 16)
  • models with a dominant diagonal (mostly self-interaction, in clusters 1 to 3)
  • models where the central location does not receive any flow (clusters 4 and 9)
  • more complex patterns in clusters 5 to 8, and 10 to 12

We can gain further insight into the different behaviours using the location positions, provided we focus on the destination flows.

grid_var_autoplot(models_df, cluster,
  flows = "destination",
  with_positions = TRUE
) +
  scale_size_continuous(range = c(0, 4)) +
  coord_fixed()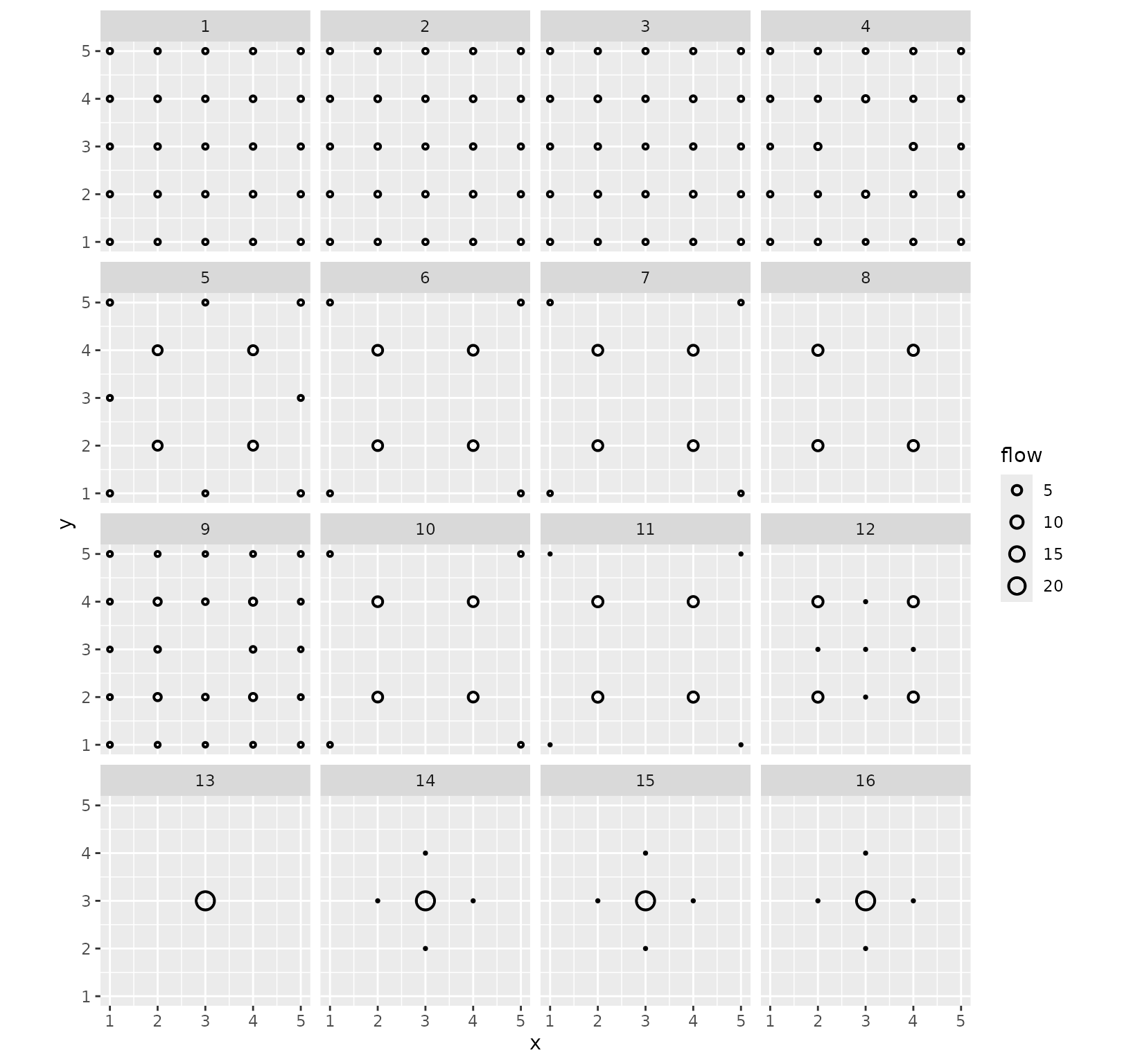

A 4x4 grid of 16 spatial variability plots showing destination flow patterns across a 5x5 coordinate grid for each model cluster. Each plot is a position based standard variability plot. Subplots 13-16 exhibit high central dominance with a large circle at (3,3); subplots 1-3 show uniform flows across all internal locations; subplots 4 and 9 show an empty center; and subplots 5-12 display varying regional hub patterns at coordinates (2,2), (2,4), (4,2), and (4,4)

The fact that we see only one circle at most per position illustrates the quality of the clusters (this was also the case in the previous visualisation, but less clearly). Indeed, this means that the destination flows are almost constant in each cluster of models. Moreover, this representation, while blind to the actual pairwise flows, shows the structure of the clusters. In particular, it emphasises subtle differences between cluster 13 and clusters 14 to 16 (and similarly for e.g. clusters 10 and 11).

Finding representative models

In addition to the variability plots, one may want to extract some representative examples from each cluster. The median.sim_list() function provides a solution based on the concept of generalised median (also called medoid): the function returns, from a collection of spatial interaction models in a sim_list(), the one that is on average the closest to all the other models. The distance used is one of the distances provided by grid_distance(). It is recommended to use the same distance for clustering, but this is not enforced by the function (as it applies to any sim_list()). In practice, we use tapply() to compute a list of medoids, and then build a sim_list() and a sim_df().

models_centre <- sim_list(tapply(models, models_df$cluster,
  median,
  flows = "destination"
))
models_centre_df <- sim_df(models_centre)

This small collection of models can then be displayed exhaustively, using grid_autoplot(). This function uses ggplot2::facet_wrap() to show a standard spatial interaction model graphical representation (the ones provided by autoplot.sim()) for each of the models in a sim_df. For instance, one can get the flows of all medoids as follows.

grid_autoplot(models_centre_df) +
  scale_fill_gradient(low = "white", high = "black") +
  coord_fixed()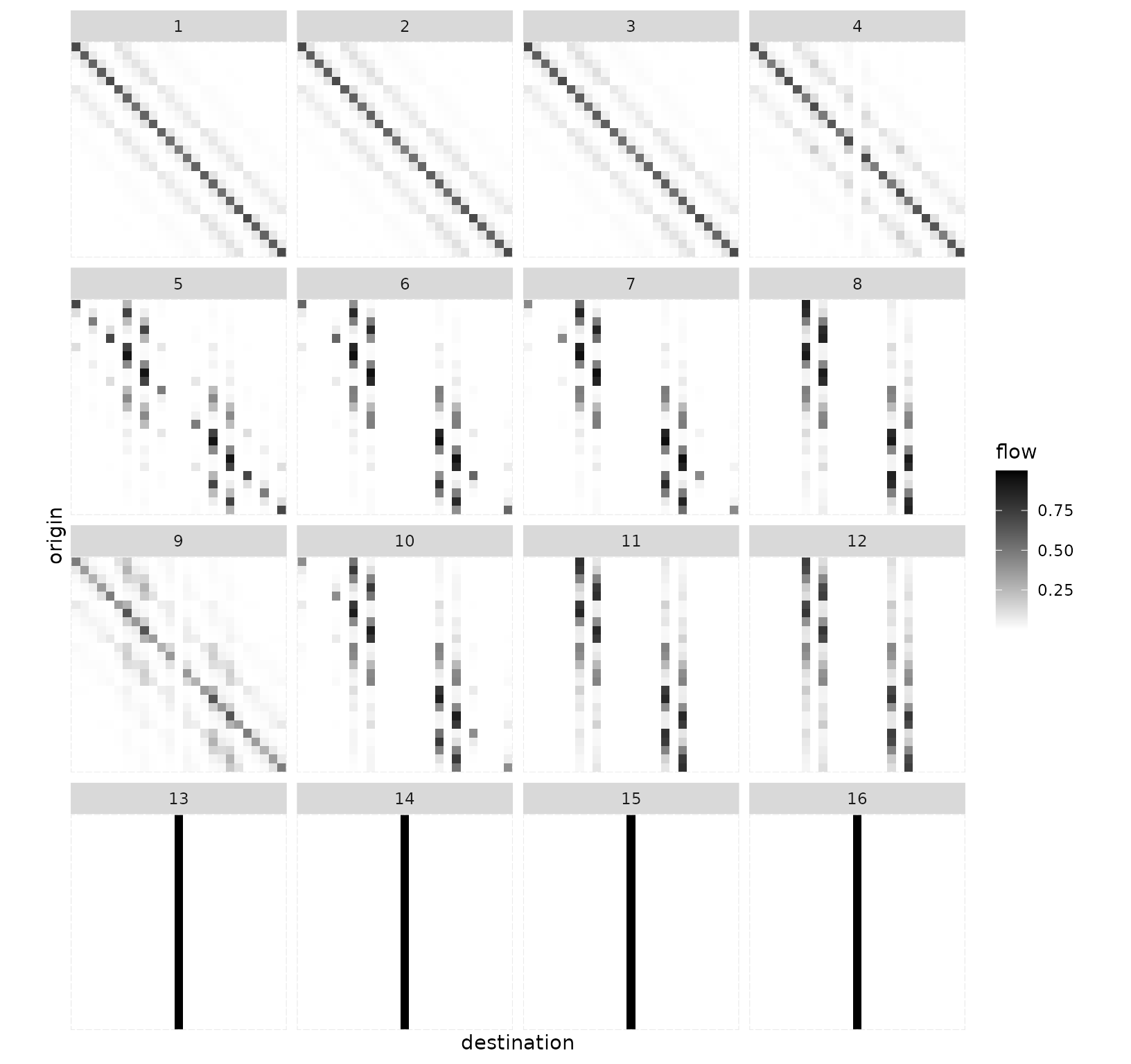

A 4x4 grid of 16 flow matrices showing the flows of medoid of each cluster using a grayscale gradient to represent flow intensity. Subplots 1-3 show a strong black diagonal indicating high self-interaction; Subplots 4 and 9 show also a diagonal structure but without any flow going to the central position M; subplots 5-8 and 10-12 feature vertical dark bands at regional hub locations G, I, Q, and S; and subplots 13-16 display a singular, solid black vertical line at the center (location M), illustrating absolute central dominance.

The function supports all the individual representations, for instance flows with positions.

grid_autoplot(models_centre_df,
  flows = "full", with_positions = TRUE,
  arrow = arrow(length = unit(0.015, "npc"))
) +
  scale_linewidth_continuous(range = c(0, 0.5)) +
  coord_fixed()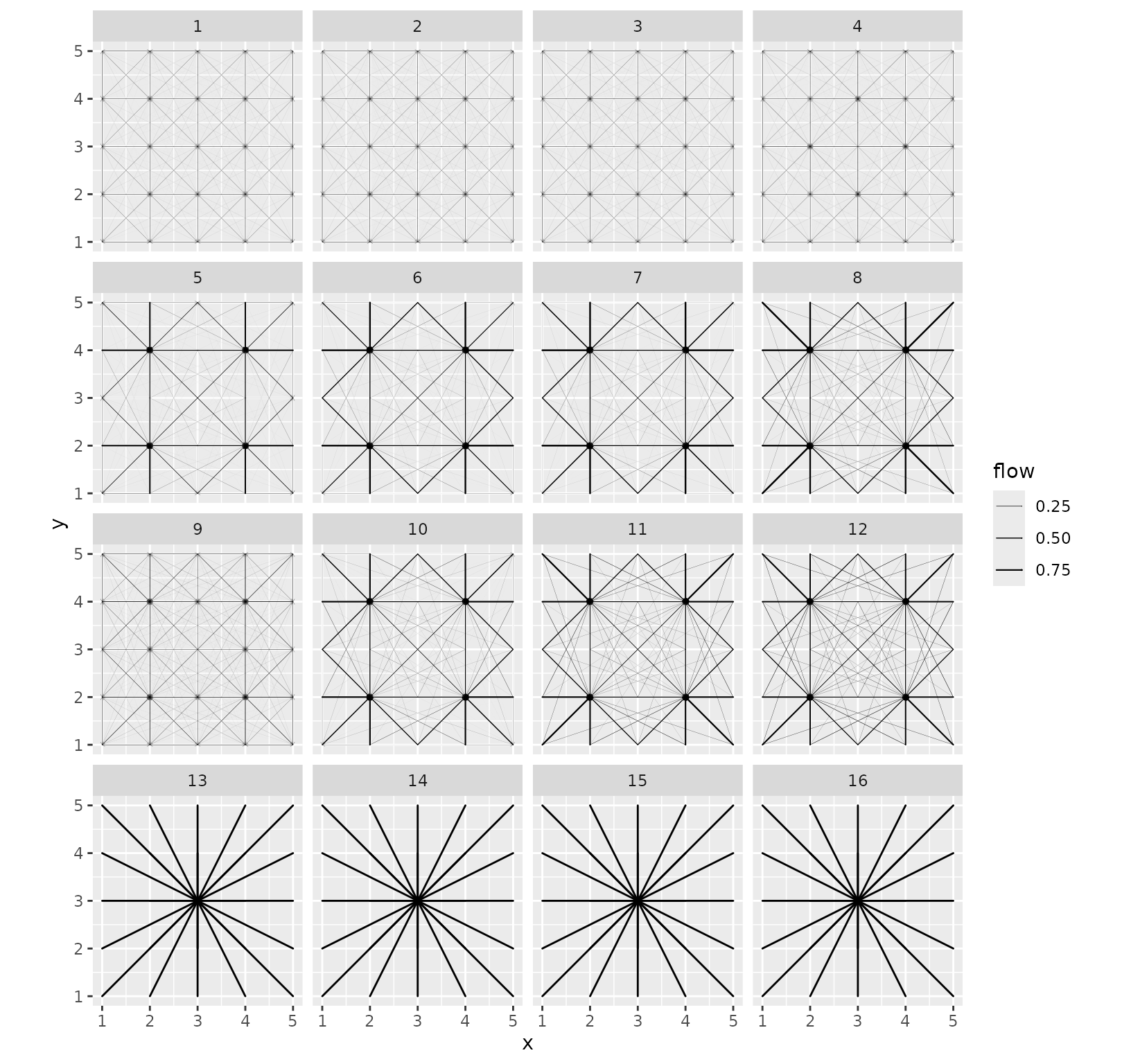

A 4x4 grid of 16 dot and arrow representations showing the flows of the medoid of each cluster. The figure displays patterns consistent with the analysis conducted on the previous figure.

Destination flows with positions are also supported.

grid_autoplot(models_centre_df, flows = "destination", with_positions = TRUE) +
  scale_size_continuous(range = c(0, 6)) +
  coord_fixed()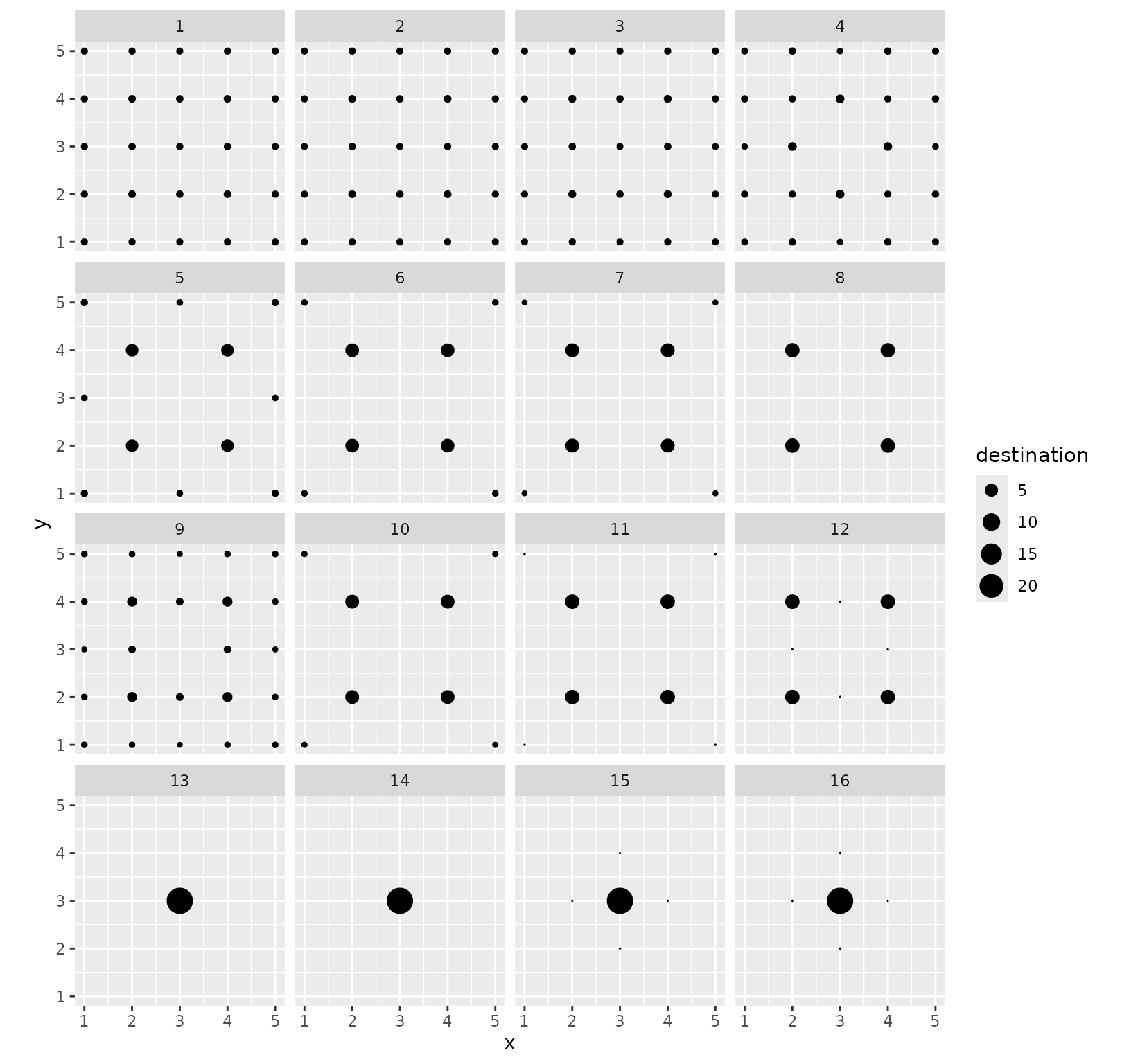

A 4x4 grid of 16 dot representations showing the destination flows of the medoid of each cluster. The figure displays patterns consistent with the analysis conducted on the previous figure, for instance a dot at each position for clusters 1 to 4, emphasizing self interaction only.

In this example, the structure of the result collection is quite simple and was already captured to a large extent by the variability plots. In more complex situations, the series of graphics are complementary and give a better insight into the solution space.

Real-world examples

European cities

Let us analyse the eurodist dataset, which consists of road distances between 21 cities in Europe. We use approximate coordinates of those cities obtained from OpenStreetMap.

data("eurodist")
eurodist_names <- labels(eurodist)
eurodist_names[match("Lyons", eurodist_names)] <- "Lyon"
eurodist_names[match("Marseilles", eurodist_names)] <- "Marseille"
eurodist_mat <- as.matrix(eurodist)
colnames(eurodist_mat) <- eurodist_names
rownames(eurodist_mat) <- eurodist_names
eurodist_coord <- data.frame(
  longitude = c(
    23.7337556, 2.14541, 4.3386684, 1.8110332, -1.5839619,
    6.94851185, 12.56571, 6.12186775, -5.3482947, 10.1185387,
    4.1148457, -9.1655069, 4.83042935, -3.7034351, 5.3805535,
    8.90758575, 11.6032322, 2.3222823, 12.5451136, 18.0710935,
    16.37833545
  ),
  latitude = c(
    37.9726176, 41.31120535, 50.89415265, 50.9338734, 49.6456093,
    50.84446155, 55.67613, 46.20823855, 36.1113418, 53.57845325,
    51.96912755, 38.7076287, 45.7591956, 40.47785335, 43.28032785,
    45.48039615, 48.1235428, 48.8787706, 41.8983351, 59.3251172,
    48.1653537
  ),
  name = eurodist_names
)

This yields the following map.

ggplot(eurodist_coord, aes(longitude, latitude, label = name)) +
  geom_point() +
  ggrepel::geom_label_repel() +
  coord_sf(crs = "epsg:4326")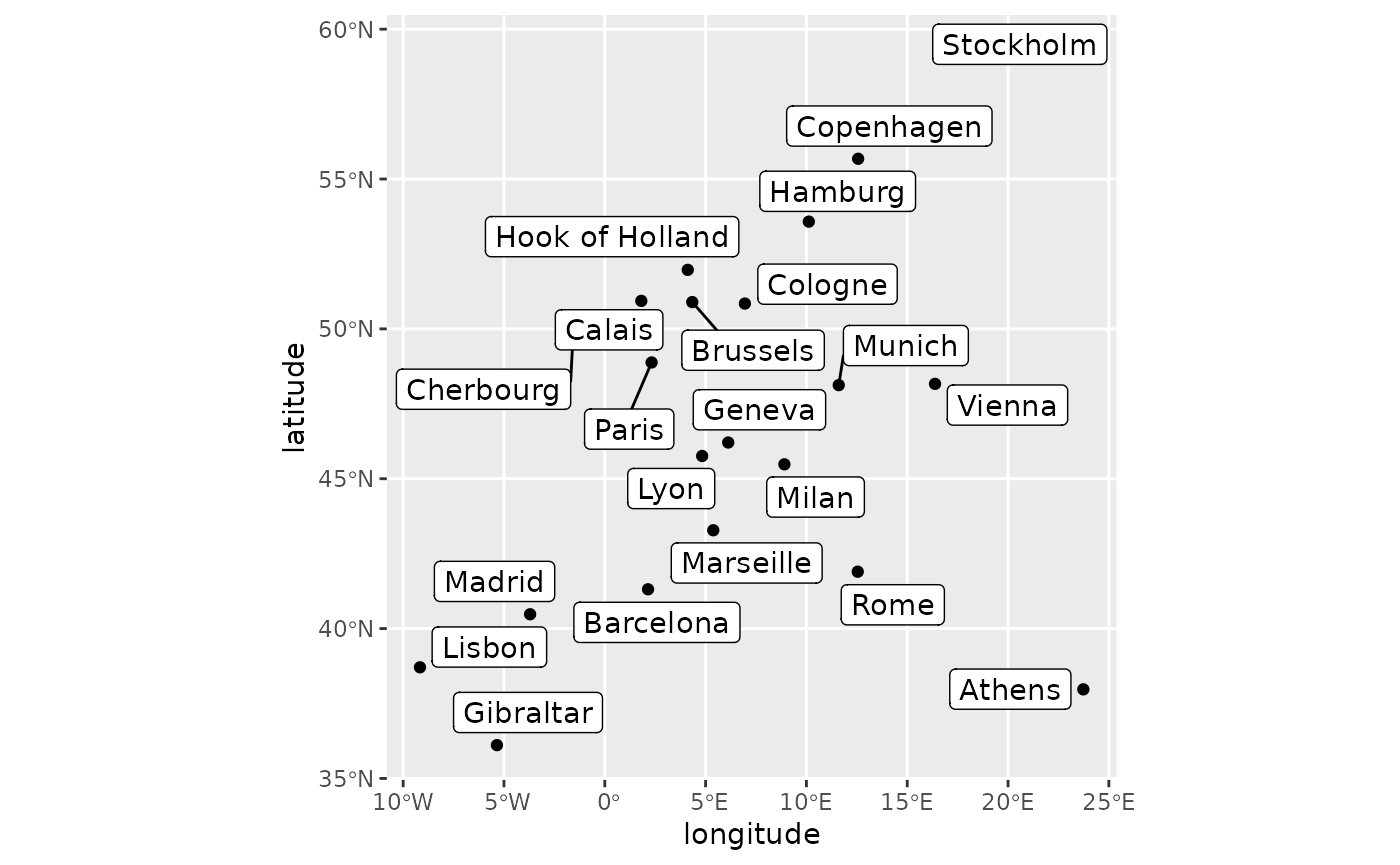

A geographical map of the 21 cities under study. Central cities include Lyon and Geneva. On the extreme east, we have Stockholm in the north and Athens in the south. On the extreme west, we have Gibraltar and Lisbon, both in the south of the region.

Models

We fit a collection of SIMs with a wide range of values for both parameters.

euro_models <- grid_blvim(eurodist_mat,
  rep(1, 21),
  alphas = seq(1.05, 1.75, length.out = 30),
  betas = 1 / seq(50, 750, length.out = 30),
  rep(1, 21),
  bipartite = FALSE,
  epsilon = 0.05,
  iter_max = 40000,
  conv_check = 50
)
destination_positions(euro_models) <- as.matrix(eurodist_coord[1:2])
euro_models_df <- sim_df(euro_models)

Most parameter pairs lead to relatively fast convergence, with the exception of a few values.

autoplot(euro_models_df, iterations) +
  scale_fill_viridis_c()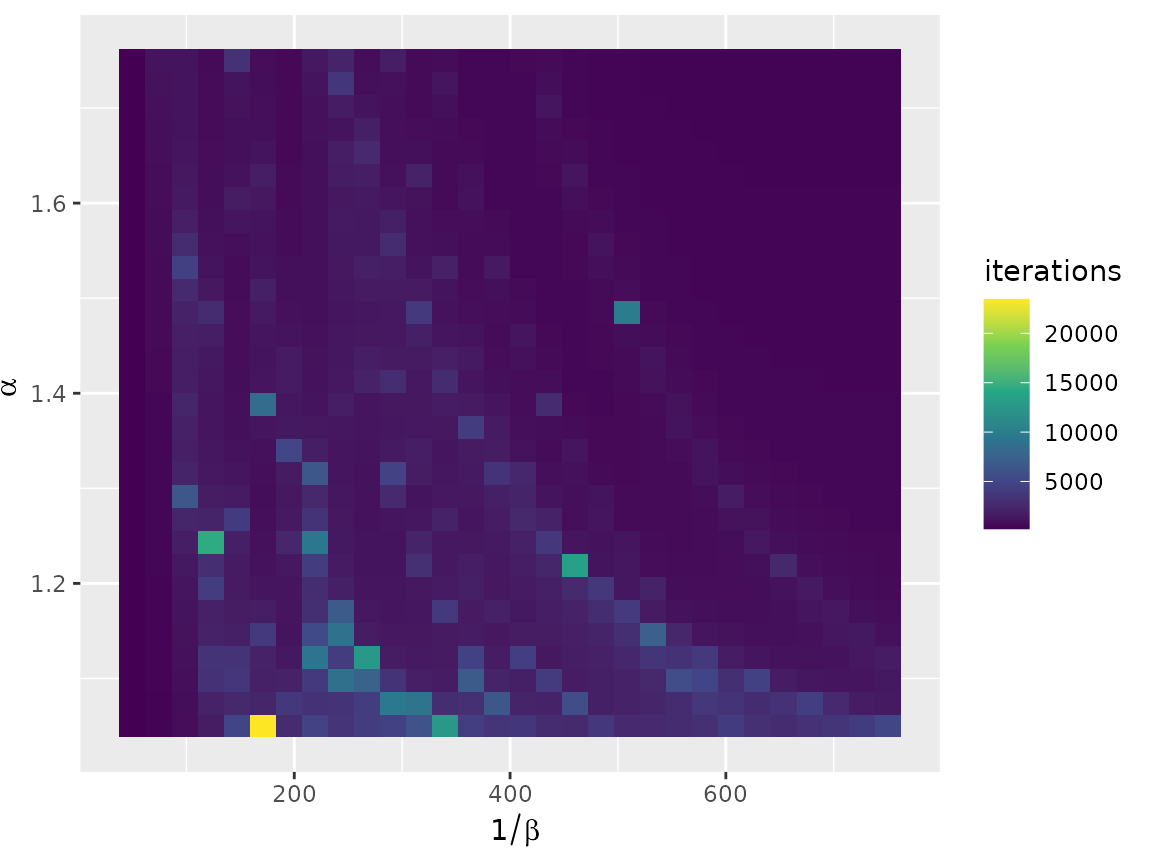

A heatmap plot showing the iteration numbers relative to two model parameters: alpha (return to scale) on the y-axis (ranging from 1.05 to 1.75) and one over beta (cost scale) on the x-axis (ranging from 50 to 750). Iteration numbers are represented by a color gradient, where dark purple indicates fast convergence (200 iterations) and bright yellow indicates slow convergence high (up to almost 24000). The plot reveals that most models are obtained quickly, with a few exceptions associated to low values of the return to scale parameter and medium to low values of the cost scale.

The full range of diversity possible with 21 cities is covered in the parameter space, which indicates that extending the parameter range will unlikely uncover SIMs that differ significantly from those obtained with the chosen range.

autoplot(euro_models_df, diversity) +
  scale_fill_viridis_c()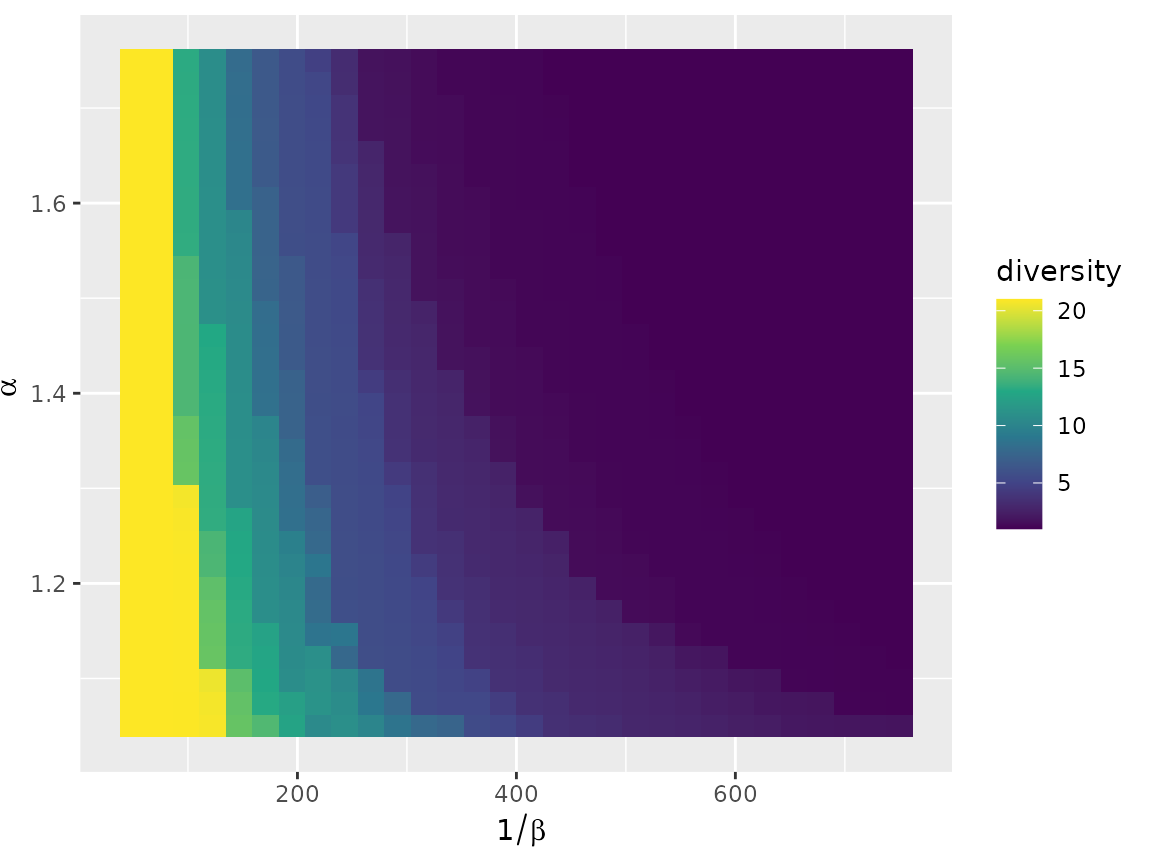

A heatmap plot showing the diversity of incoming flows relative to two model parameters: alpha (return to scale) on the y-axis (ranging from 1.05 to 1.75) and one over beta (cost scale) on the x-axis (ranging from 50 to 750). Diversity values are represented by a color gradient, where dark purple indicates a low diversity (starting at 1) and bright yellow indicates maximal diversity (21). The plot shows that a large part of the parameter space corresponds to concentrated flows into a single destination with a very low diversity (for high values of the cost scale). A reduction of the cost scale induces an increase of the diversity, with an additional less pronounced increase associated to reducing the return to scale parameter. When the cost scale parameter is below approximately 100, the diversity is maximal for all values of the return to scale parameter.

Variability plot

The flow variability plot outlines a few cities as potentially dominant. Lyon is the strongest. This is explained by its central position on the map. We expect to find it as the single dominant city in many configurations. Hook of Holland and Brussels also appear, but to a lesser extent. Gibraltar is also potentially active in some configurations. Athens and Stockholm are frequently the sole recipients of their own flow, probably owing to their isolated positions.

autoplot(euro_models, with_names = TRUE) +
  theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust = 1))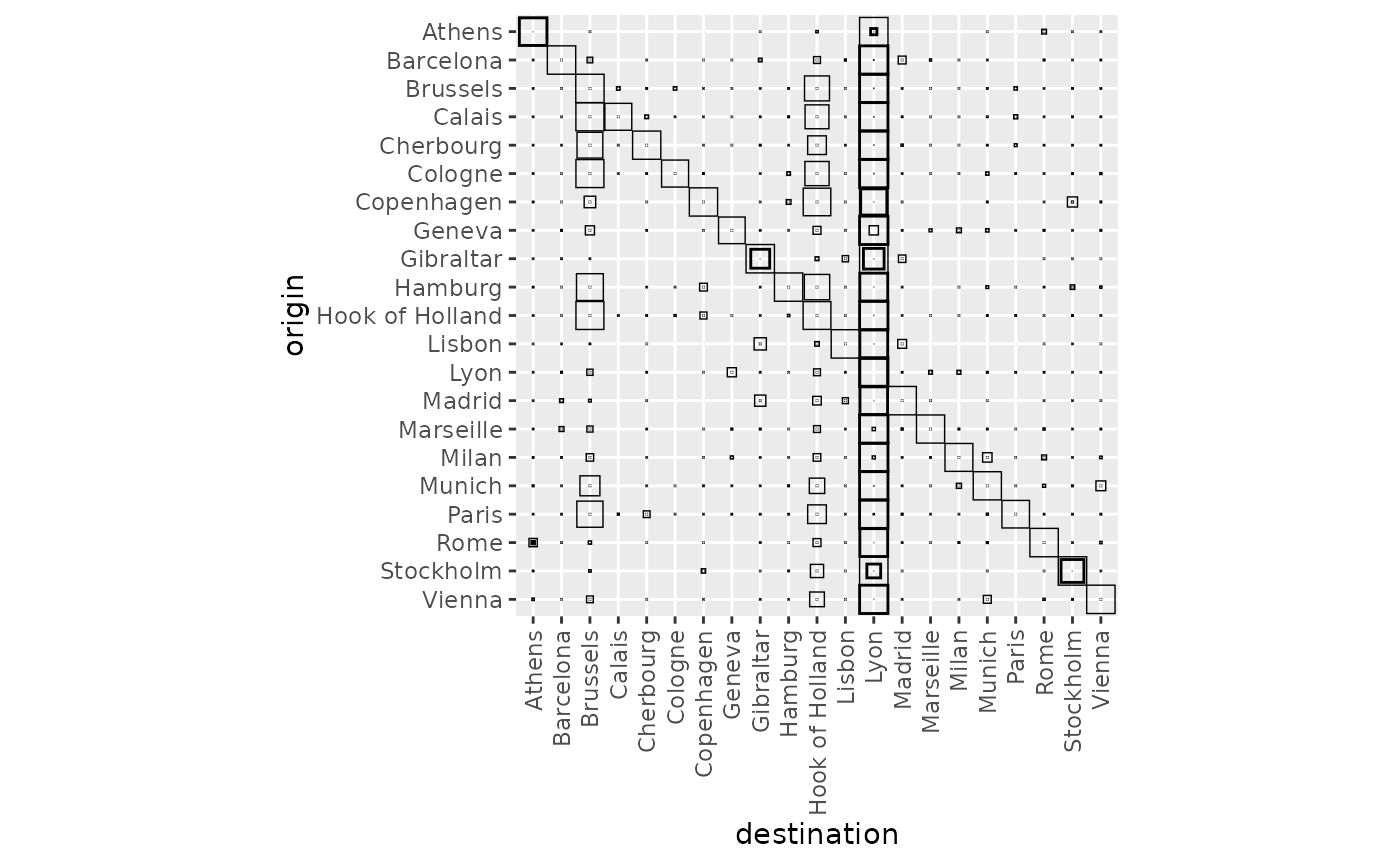

A variability plot matrix for flows between European cities. The central destination, Lyon, is represented by a solid vertical column of thick-bordered squares, indicating high median flow from all origins. Secondary hubs like Brussels and Hook of Holland show smaller clusters of flow activity, while most other cities receive little to no incoming flow across the models.

Destination flows tell the same story. Notably, most of the cities have a null median incoming flow, apart from Athens, Gibraltar, Lyon and Stockholm. In addition, most of the cities have a 0.95 quantile of 1, which corresponds to local configurations, that is situations when \(\beta\) is large enough to prevent any external flows. Only Brussels and Hook of Holland stand out (in addition to the four cities mentioned above).

autoplot(euro_models, flows = "destination", with_names = TRUE) +
  coord_flip()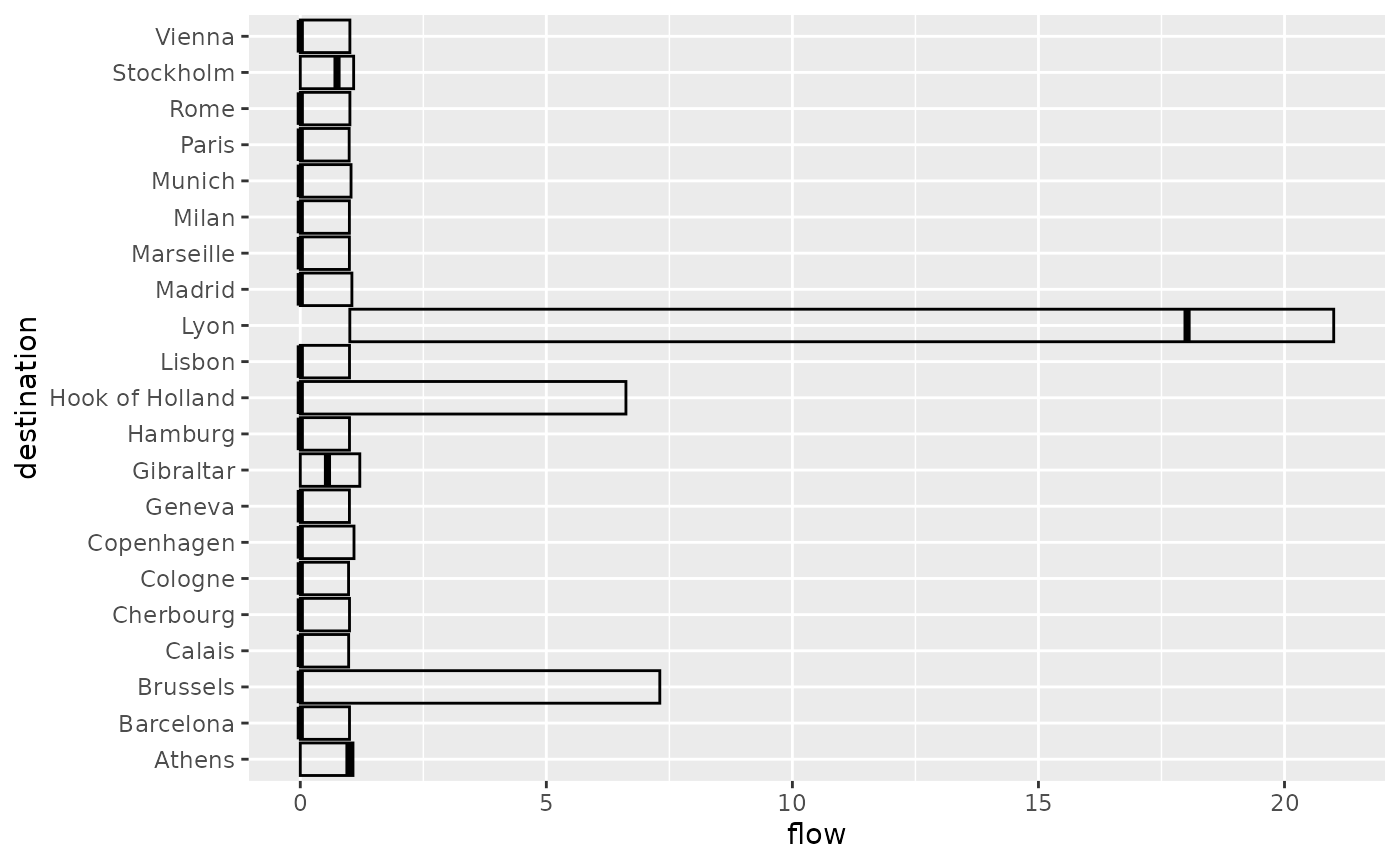

A horizontal bar chart displaying flow statistics for 21 European destinations. Lyon dominates the chart with a significantly longer bar than any other city, reaching a flow value over 20 (and a median over 17). Brussels and Hook of Holland show moderate maximum flow levels (approx 7), while cities like Athens, Gibraltar and Stockholm show non zero median incoming flow. minimal activity. All other cities have a zero median flow and a maximal incoming flow of one.

autoplot(euro_models,
  flows = "destination", with_positions = TRUE,
  with_names = TRUE
) +
  scale_size_continuous(range = c(0, 6)) +
  coord_sf(crs = "epsg:4326")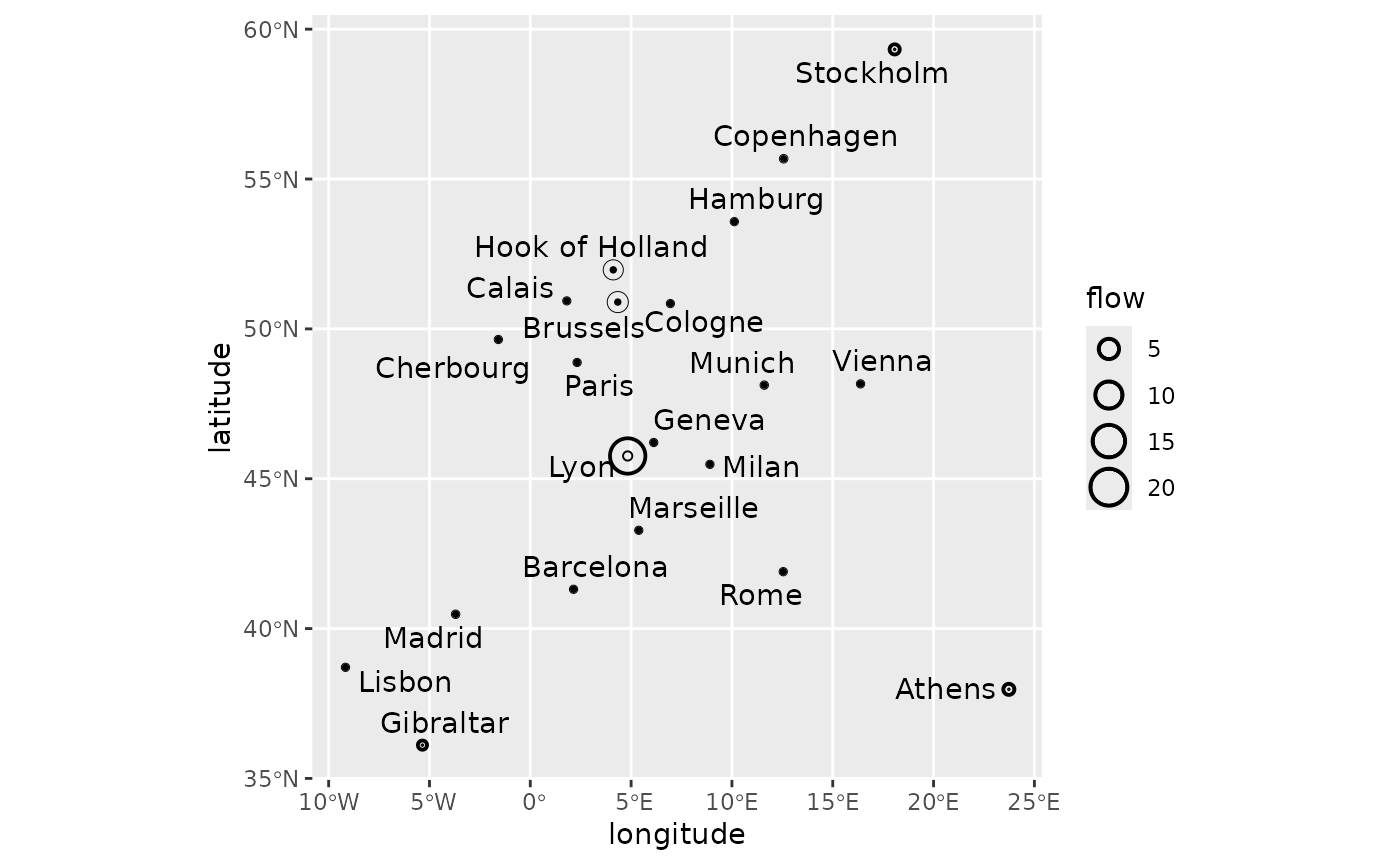

A geographic plot of Europe where flow statistics for 21 cities are represented by circles of varying sizes and thicknesses. Lyon features the largest, thickest circle at approximately 5°E, 45°N, indicating it is the primary destination hub. Secondary hubs like Brussels and Hook of Holland are marked with medium-sized circles, while most other cities, such as Rome and Madrid, appear as small dots. The figure tells essentially the same story as the previous one by in a geographic settings. This emphasizes the central position of Lyon, as well as the extreme positions of cities with non zero median incoming flow (Athens, Gibraltar and Stockholm).

Clustering

We apply the same clustering strategy as with the artificial data: 16 clusters obtained with hierarchical clustering using the Ward criterion.

euro_models_dist <- sim_distance(euro_models, "destination")
euro_models_hc <- hclust(euro_models_dist, method = "ward.D2")

The dendrogram clearly shows three main clusters, but as explained above, the role of clustering is to facilitate exploration of the result spaces rather than to identify distinct clusters.

plot(euro_models_hc, hang = -1, labels = FALSE)

A Cluster Dendrogram for European city models using the ward.D2 method. The tree splits into two primary branches at a height of approximately 350. The left branch is a dense, large cluster representing highly similar models, while the right branch is further subdivided into several smaller, more distinct groups at heights between 50 and 150, indicating higher variability among those model classes.

The clusters are well organised on the parameter set.

euro_models_df$cluster <- as.factor(cutree(euro_models_hc, k = 16))
autoplot(euro_models_df, cluster) +
  theme(legend.position = "bottom") +
  guides(fill = guide_legend(nrow = 2))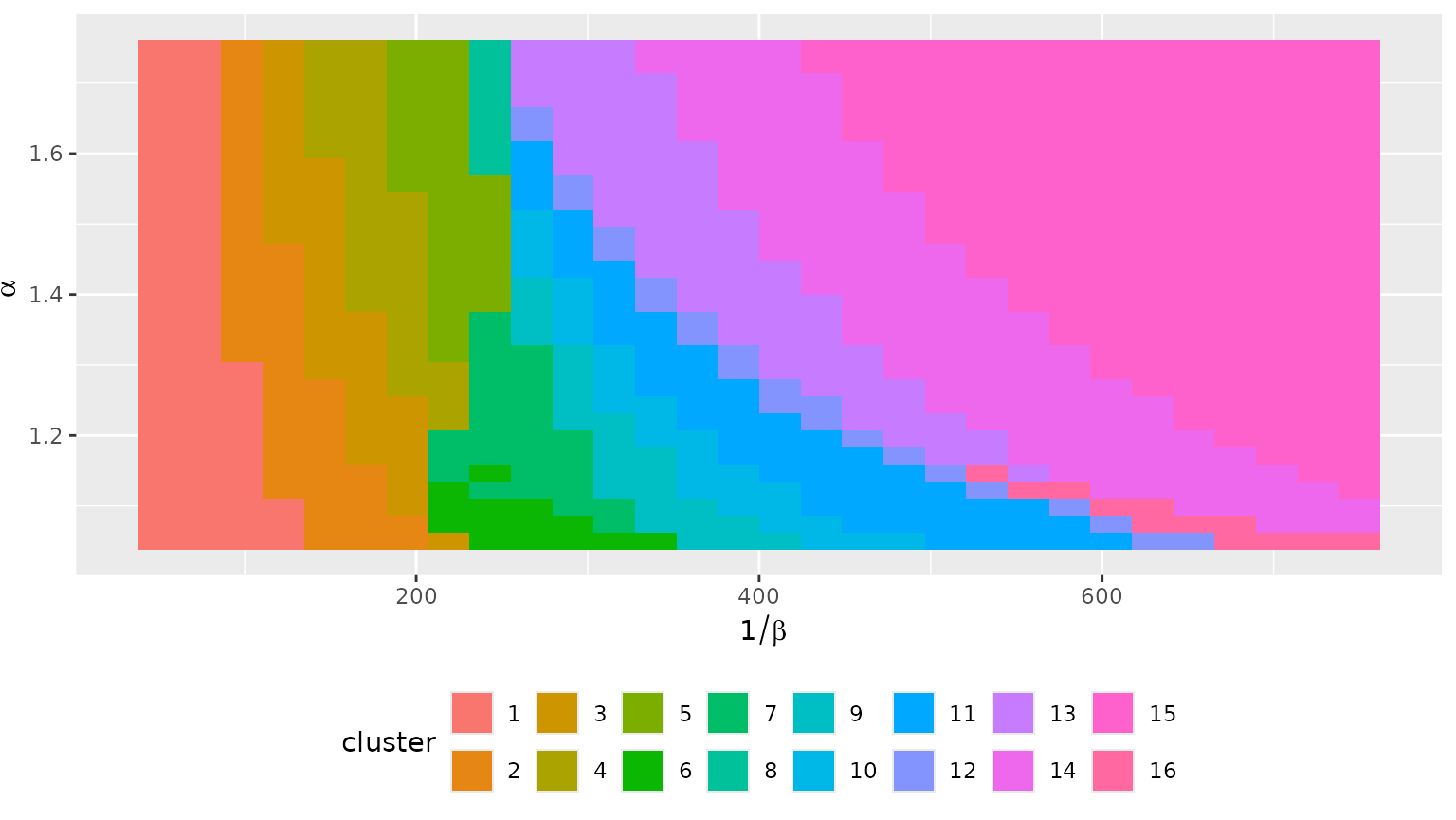

A heatmap showing the distribution of 16 clusters across a parameter space defined by alpha (y-axis) and 1/beta (x-axis) for European city models. The clusters are organized in distinct vertical and diagonal bands. Cluster 15 (pink) dominates the right side of the space where 1/beta is high (above 600), while clusters 1 through 7 occupy the left side of the plot where 1/beta is low (below 300).

The variability plot shows mostly isolated circles with no inner or outer ring. This means that the clusters are relatively homogeneous in terms of destination flows, and thus median flows will give a good idea of typical behaviours.

grid_var_autoplot(euro_models_df, cluster,
  flows = "destination",
  with_positions = TRUE
) +
  scale_size_continuous(range = c(0, 6)) +
  coord_sf(crs = "epsg:4326")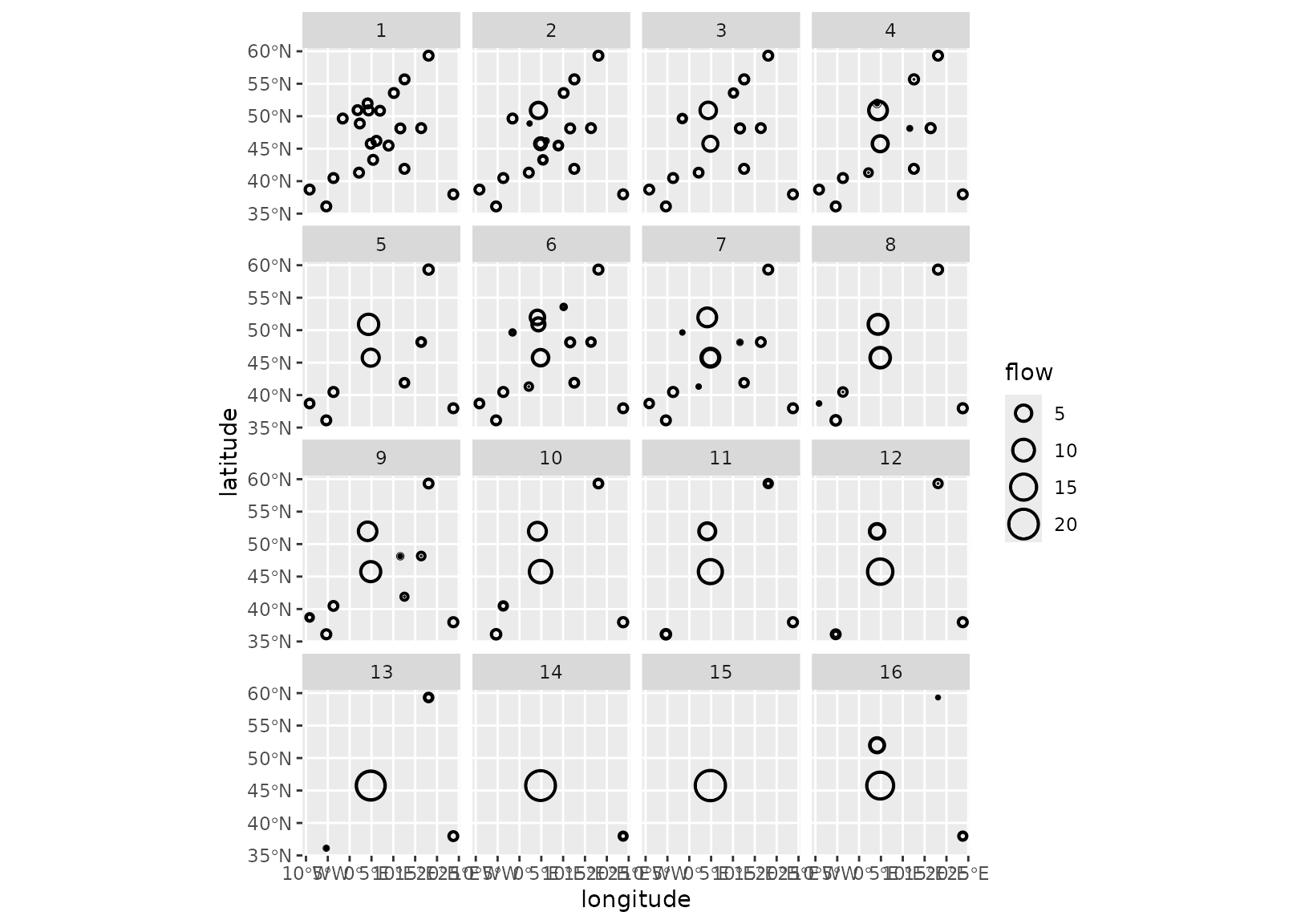

A 4x4 panel showing spatial flow circles for each of the 16 clusters on a map of Europe. In clusters 13-15, a single large circle at Lyon dominates the map. Clusters 1-4 show many small, uniform circles across all 21 city locations. Clusters 5-12 show a mix of hubs, with larger circles appearing at different locations like Brussels and Hook of Holland (clusters 4 and 6).

Those behaviours are visible both at the destination flow level (above) and at the flow level (below):

  • Clusters 1 to 3 correspond to situations where most of the flows are local (hence the importance of the diagonal flow), with a progressive shift towards sending flow to Lyon. Brussels is also important in clusters 2 and 3.
  • Clusters 4, 6 and 7 maintain a relatively strong diagonal (self) flow with more flows sent to Lyon and a transition between Brussels and Hook of Holland
  • Clusters 5, 8 and 9 are intermediate situations where some cities play the role of local attractors, e.g., Rome and Vienna, but the concentration on external cities and Lyon and Brussels (5 and 8) or Hook of Holland (9) is progressing.
  • Clusters 10 to 12 are situations where both Lyon and Hook of Holland share incoming flows, with more (10) or fewer (12) flows reaching external cities such as Stockholm, Athens and the trio Gibraltar, Lisbon and Madrid.
  • Clusters 13 to 15 show Lyon as the dominating city, while in cluster 16, Lyon shares its incoming flow with Hook of Holland.
grid_var_autoplot(euro_models_df, cluster)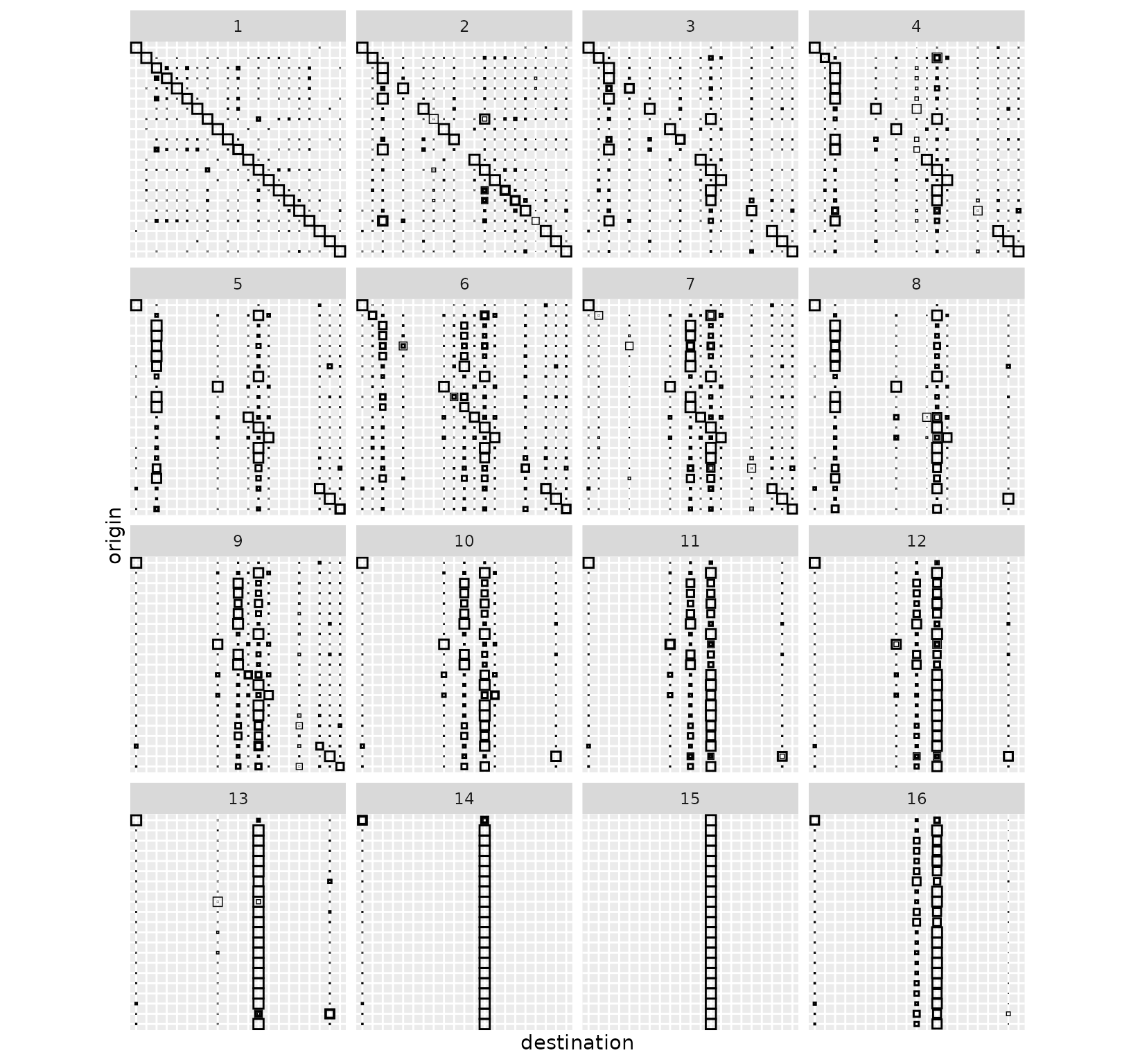

A 4x4 panel of 16 matrix plots showing flow variability for each cluster of European city models. Clusters 13-15 exhibit high central dominance with a single thick vertical line at the Lyon destination. Clusters 1-4 show stronger activity along the diagonal, representing internal city flows, while clusters 5-12 and 16 show diverse patterns with multiple vertical hub lines at cities like Brussels and Hook of Holland.

Medoids

Finally, we look at medoids.

euro_models_centre <- sim_list(tapply(euro_models, euro_models_df$cluster,
  median,
  flows = "destination"
))
euro_models_centre_df <- sim_df(euro_models_centre)

The medoids confirm the analysis given above.

grid_autoplot(euro_models_centre_df) +
  scale_fill_gradient(low = "white", high = "black") +
  coord_fixed()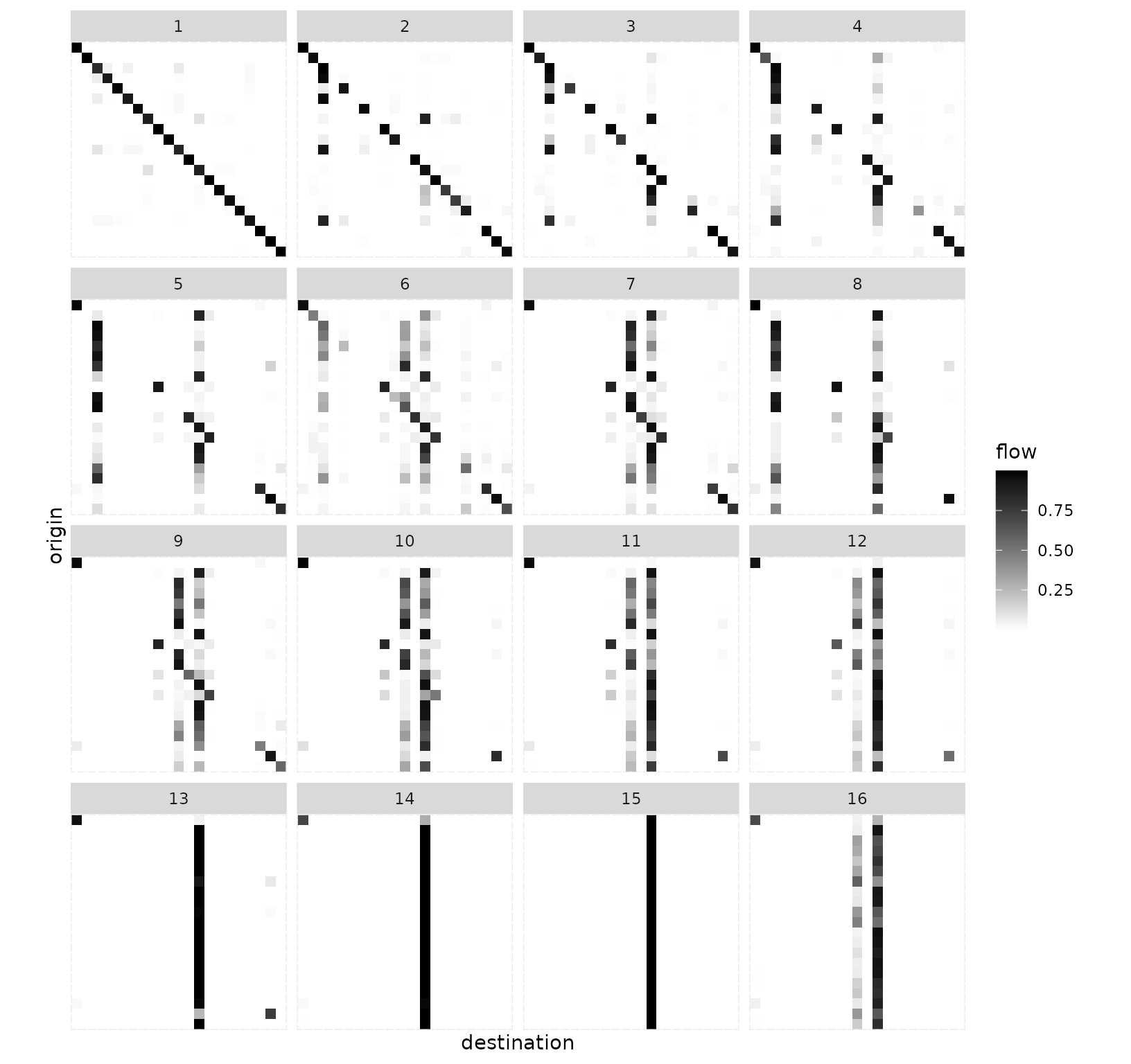

4-by-4 faceted grid of flow matrices, one per cluster medoid. Each heatmap shows origin nodes on the y-axis and destination nodes on the x-axis. From the top-left facet to the bottom-right, the flows transition from a diagonal distribution (local/internal flows) to sharp vertical lines, indicating that all origins are sending their flows to a few dominant destination 'hubs'. This is consistent with previous analyses.

grid_autoplot(euro_models_centre_df,
  flows = "destination",
  with_positions = TRUE
) +
  scale_size_continuous(range = c(0, 6)) +
  coord_sf(crs = "epsg:4326")

4-by-4 faceted grid of destination flows geographical representation, one per cluster medoid. The representation is very similar to the variability plots of the clusters confirming previous analyses.

grid_autoplot(euro_models_centre_df,
  with_positions = TRUE, arrow = arrow(length = unit(0.015, "npc"))
) +
  scale_linewidth_continuous(range = c(0, 0.75)) +
  coord_sf(crs = "epsg:4326")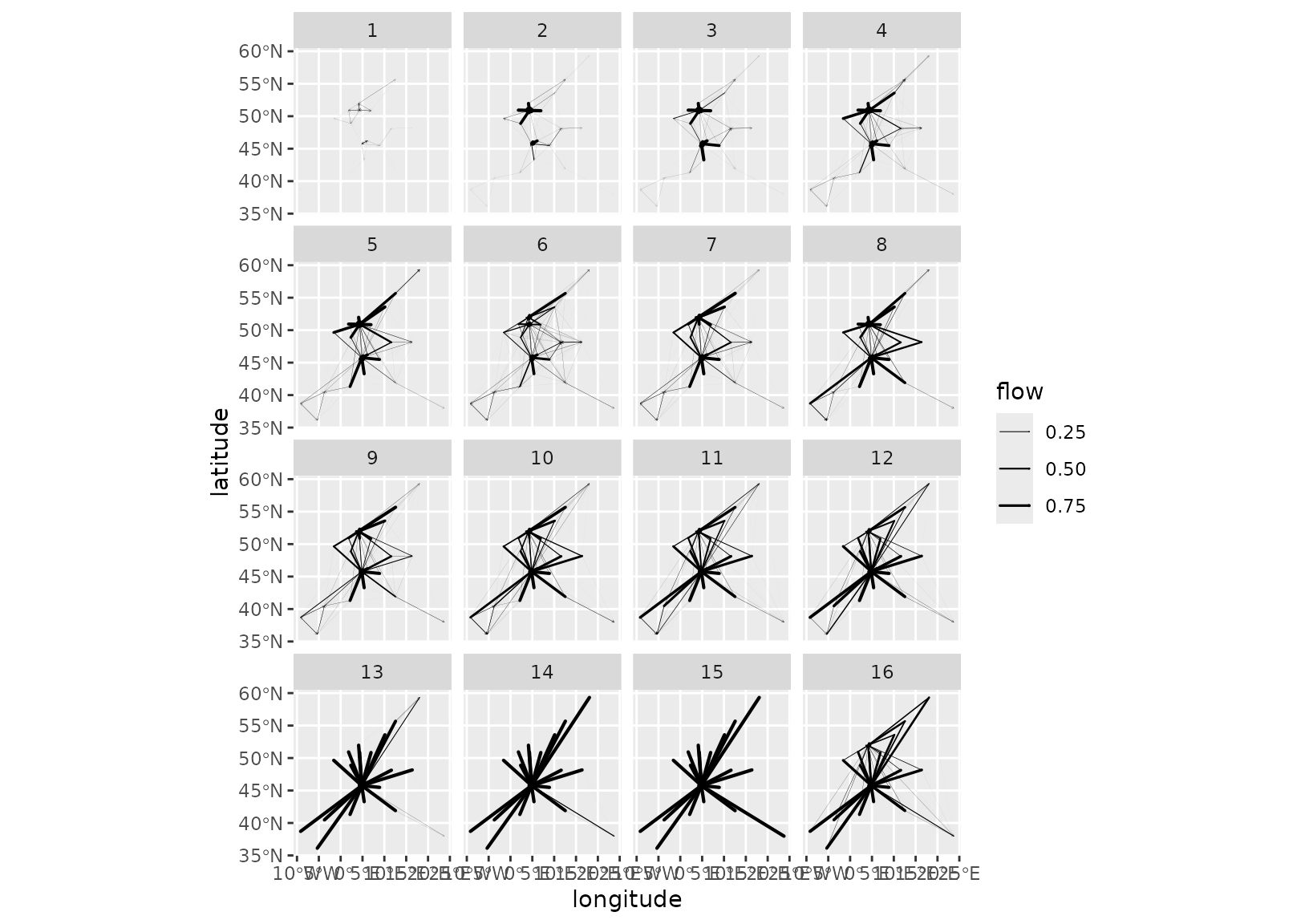

A 4x4 grid of 16 dot and arrow representations showing the flows of the medoid of each cluster. The plots complement the previous analyses by emphasizing the exchange patterns. There are two main regimes. Clusters 1 to 12, and 16, corresponds approximately to a dual regime with exchanges in the north of Europe and exchanges in the south of Europe, both parts being dominated by a central city (that changes from cluster to cluster). Clusters 13 to 15 display the other regime in which Lyon dominates and receive all the circulating flow.

To further the analysis, one can focus on a particular medoid, for instance cluster 1:

autoplot(euro_models_centre[[1]],
  flows = "full", with_positions = TRUE,
  arrow = arrow(length = unit(0.015, "npc"))
) +
  scale_linewidth_continuous(range = c(0, 2)) +
  coord_sf(crs = "epsg:4326")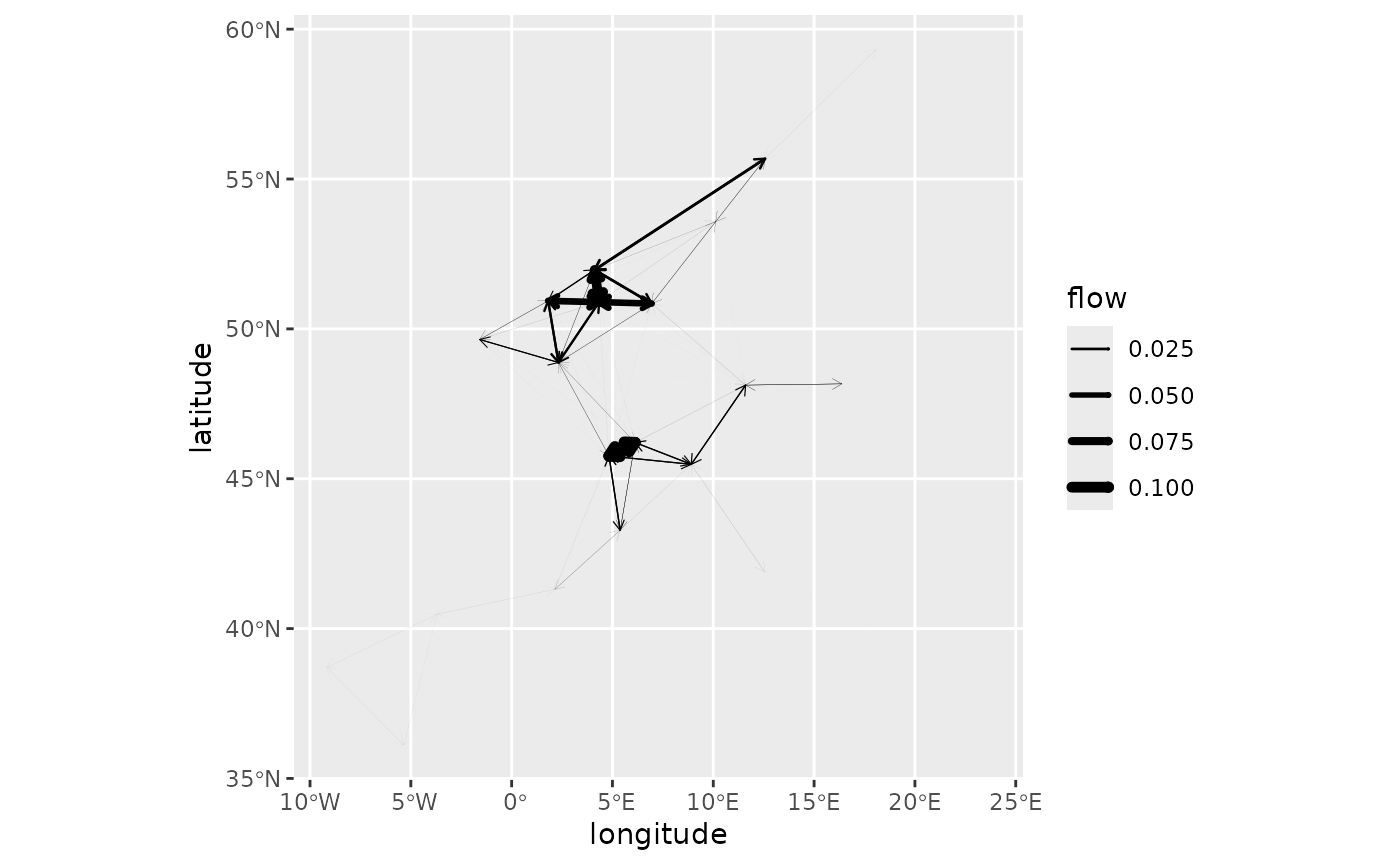

A detailed spatial network plot showing directed flows. Thick black arrows indicate high-volume flows between central nodes, while thin, light-grey lines represent minor flows. The network is organized into two distinct clusters of activity in the upper and lower central regions. Flow values are small, as most of the global flow is self-directed and not shown on the figure.

Or cluster 5:

autoplot(euro_models_centre[[5]],
  flows = "full", with_positions = TRUE,
  arrow = arrow(length = unit(0.015, "npc"))
) +
  scale_linewidth_continuous(range = c(0, 2)) +
  coord_sf(crs = "epsg:4326")

A high-intensity spatial network plot. Thick black lines dominate the center of the map, forming a dense web of high-volume flows between a small number of attractive destinations, while peripheral nodes are connected by only very thin, faint lines. This illustrate a typical case of north and south exchanges.

Finally, one can randomly select a subset of the models in a cluster and use grid_autoplot() to display these models all at once. This offers a way to visually assess the variability within that cluster. For instance, in the figure below for cluster 4, most of the models are very similar, but some differences exist, such as the flows to Hamburg and Copenhagen, whose level varies across the configurations (compare 6 to 7, for instance).

set.seed(0)
euro_models_idx <- sample(which(euro_models_df$cluster == 4), 16)
euro_models_cl4_sample <- euro_models[euro_models_idx]
euro_models_cl4_sample_df <- sim_df(euro_models_cl4_sample)
grid_autoplot(euro_models_cl4_sample_df, with_positions = TRUE) +
  scale_linewidth_continuous(range = c(0, 1)) +
  coord_sf(crs = "epsg:4326")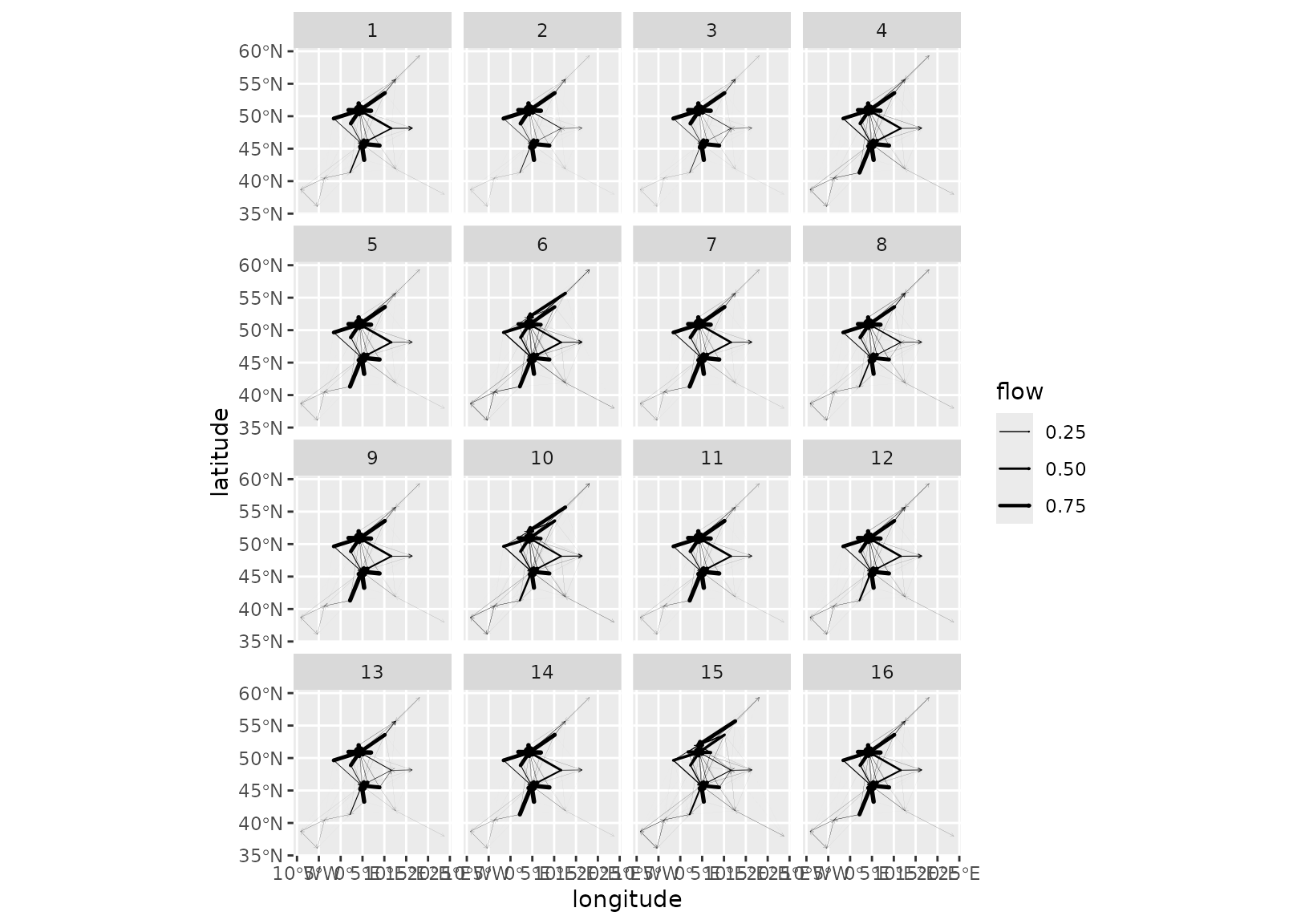

A faceted grid of network flow maps. Unlike the previous exploration, this grid shows high stability across all 16 facets. In every panel, the flow arrows are nearly identical, converging on two main central hubs, illustrating that the cluster is largely homogeneous.

French cities

We use the french_cities data set to illustrate the bipartite case when origin and destination locations differ. Here we consider flows from the largest French cities (in terms of population) to the smallest ones. As shown below, the distribution of the smallest cities is not all uniform as they cluster around large ones, especially around Paris.

big_cities <- french_cities[1:20, ]
small_cities <- french_cities[102:121, ]
fr_cities <- rbind(big_cities, small_cities)
fr_cities$type <- c(rep("origin", 20), rep("destination", 20))
ggplot(
  fr_cities,
  aes(x = th_longitude, y = th_latitude, color = type)
) +
  geom_point() +
  coord_sf(crs = "epsg:4326")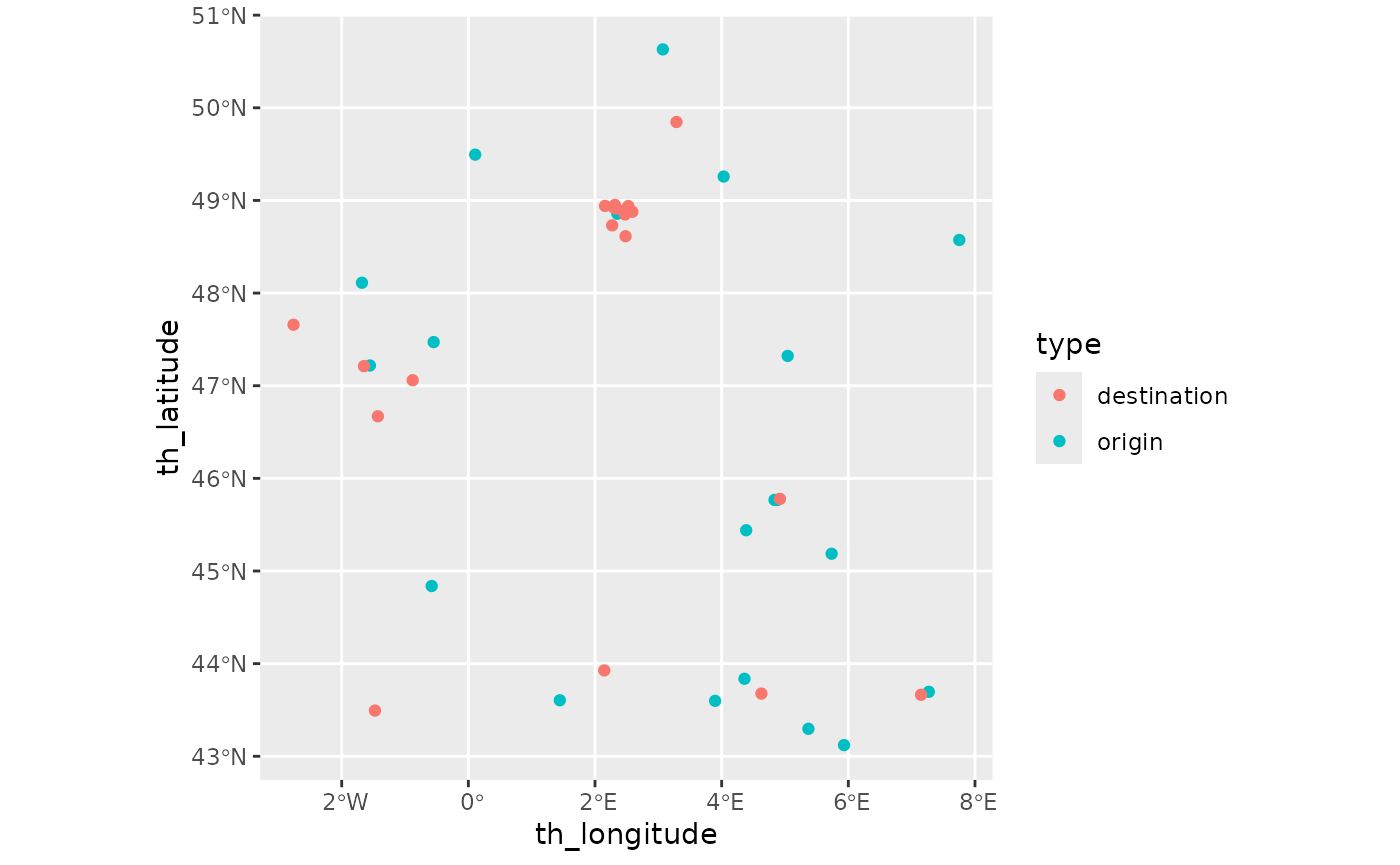

A geographic map of the 40 cities selected. The 20 largests cities are origin locations and spreaded somewhat evenly in France, excepted for a large empty region in the middle of France. The 20 smallests cities are destination locations. Half of them are clustered around Paris. Nine of the remaining ones are located south of Paris, generally in the vicinity of a large city.

Production effects 

frcosts <- french_cities_distances[1:20, 102:121] / 1000
fr_prod <- french_cities$population[1:20]
fr_attr <- rep(1, 20)
origin_data <- list(
  names = french_cities$name[1:20],
  positions = as.matrix(french_cities[
    1:20,
    c("th_longitude", "th_latitude")
  ])
)
destination_data <- list(
  names = french_cities$name[102:121],
  positions = as.matrix(french_cities[
    102:121,
    c("th_longitude", "th_latitude")
  ])
)

As we have information about the cities, we may use it to drive the model. In particular, population sizes are natural production constraints. As France is somewhat centralised, Paris is by far the largest city. The combined population of Marseille, Lyon and Toulouse is smaller than the Paris population. In addition, there is a sharp drop in population size between Toulouse, with roughly 500,000 inhabitants, and Nice with 350,000 inhabitants.

Consequently, using population sizes directly as a production constraint may lead to some extreme models. To investigate this, we use the global analysis permitted by grid_blvim() and associated functions.

We use first the logarithm of the population as the production constraint.

fr_models <- grid_blvim(frcosts,
  log(fr_prod),
  alphas = seq(1.05, 1.75, length.out = 30),
  betas = 1 / seq(5, 200, length.out = 30),
  fr_attr,
  epsilon = 0.05,
  iter_max = 40000,
  conv_check = 50,
  origin_data = origin_data,
  destination_data = destination_data
)
fr_models_df <- sim_df(fr_models)

The diversities of the models are relatively small as shown below, despite relatively short cut-off distances (the smallest value of \(\frac{1}{\beta}\) is 5 km). The degenerate patterns with bipartite models are different from the diagonal ones obtained with non-bipartite models. If we decrease the cut-off distance too much (i.e. if we use large values of \(\beta\)), each origin location will send all of its production to its nearest neighbours. Here this leads to a maximum diversity of 8.44 while in a non-bipartite case, we would expect a maximum around 20 (for 20 cities).

autoplot(fr_models_df) +
  labs(title = "Log population") +
  scale_fill_viridis_c()

A heatmap plot showing the diversity of incoming flows relative to two model parameters: alpha (return to scale) on the y-axis (ranging from 1.05 to 1.75) and one over beta (cost scale) on the x-axis (ranging from 5 to 200). Diversity values are represented by a color gradient, where dark purple indicates a low diversity (starting at 1) and bright yellow indicates maximal diversity (around 8.5). The plot shows a similar pattern as previous similar figures: decreasing the cost scale or the return to scale both increase the diversity, with more cities receiving some flow. However, the diversities themselves are significantly smaller than in the non bipartite case.

With the log transform, small cities around Paris do not receive much flow, apart for Saint-Ouen-Sur-Seine, Fontenay-sous-Bois and Sartrouville. Notice the absence of diagonal patterns. Vaulx-en-Velin receives flows from all origin locations owing to its relatively central position in France. However, its incoming flow is much more variable than in non bipartite settings with a central location.

autoplot(fr_models, with_names = TRUE) +
  theme_light() +
  theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust = 1)) +
  labs(title = "Log population")

A variability plot matrix for flows from large cities (y-axis) to small cities (y-axis). One of the main differences with the non-bipartite case is the absence of a dominant diagonal. Only Vaulx-en-Velin has an active column of squares showing that it receives a significant median incoming flows from all original locations. The matrix shows also large empty zones corresponding to cities that never receive any significant flows, for instance Vannes, Bondy and Gennevilliers.

The geographic representation emphasizes the fact that the bipartite case induces a form of local selection rather than a global one. Indeed all the destination “regions” are represented, but in each local zone, only some cities receive a significant incoming flow.

autoplot(fr_models,
  flows = "destination", with_names = TRUE,
  with_positions = TRUE
) +
  coord_sf(crs = "epsg:4326") +
  labs(title = "Log population")

A geographic plot of France where flow statistics for the 20 destination cities are represented by circles of varying sizes and thicknesses. The cities receiving flows are spreaded over the set of destination cities.

We then use the population size directly.

fr_models_direct <- grid_blvim(frcosts,
  fr_prod,
  alphas = seq(1.05, 1.75, length.out = 30),
  betas = 1 / seq(5, 200, length.out = 30),
  fr_attr,
  epsilon = 0.05,
  iter_max = 40000,
  conv_check = 50,
  origin_data = origin_data,
  destination_data = destination_data
)
fr_models_direct_df <- sim_df(fr_models_direct)

We observe a trend of smaller diversities with a maximum of 6.97. The dominance of Paris as a producer tends to limit the emergence of multiple receivers and to concentrate the flows on a smaller number of cities.

autoplot(fr_models_direct_df) +
  labs(title = "Population") +
  scale_fill_viridis_c()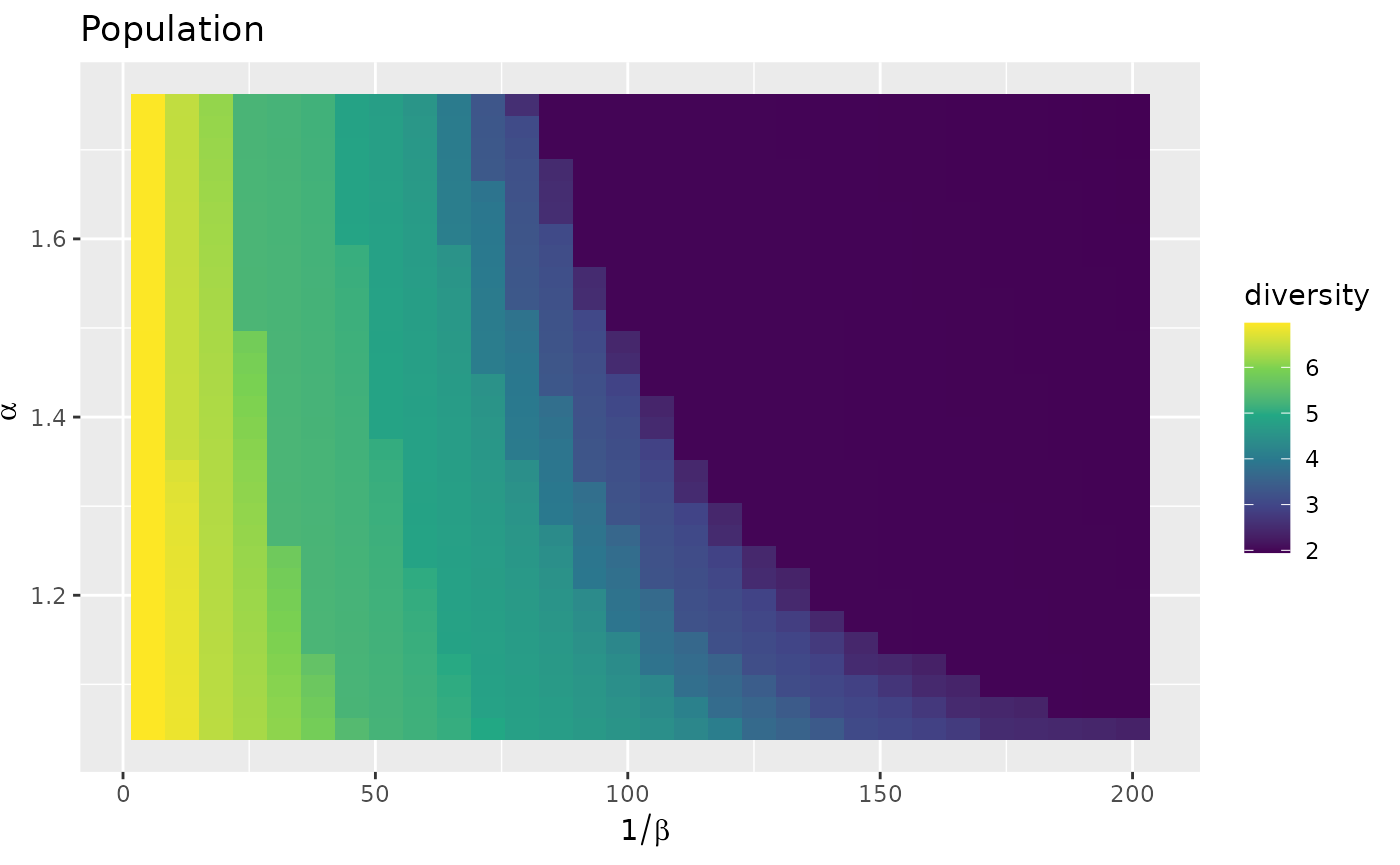

A heatmap plot showing the diversity of incoming flows relative to the model parameters. The shape of the regions of equal diversity are quite similar to the ones displayed in the previous representation, but with smaller values. There is also a larger region with a fixed diversity around 2.

In this case the flow from Paris becomes dominant and more small cities around Paris receive flow. This makes Vaulx-en-Vellin less attractive to the benefit of Saint-Ouen-sur-Seine and Arles. Globally, less cities are receiving flows. This is revealed in the graphical representation thanks to the origin based normalisation.

autoplot(fr_models_direct, with_names = TRUE, normalisation = "origin") +
  theme_light() +
  theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust = 1)) +
  labs(title = "Population")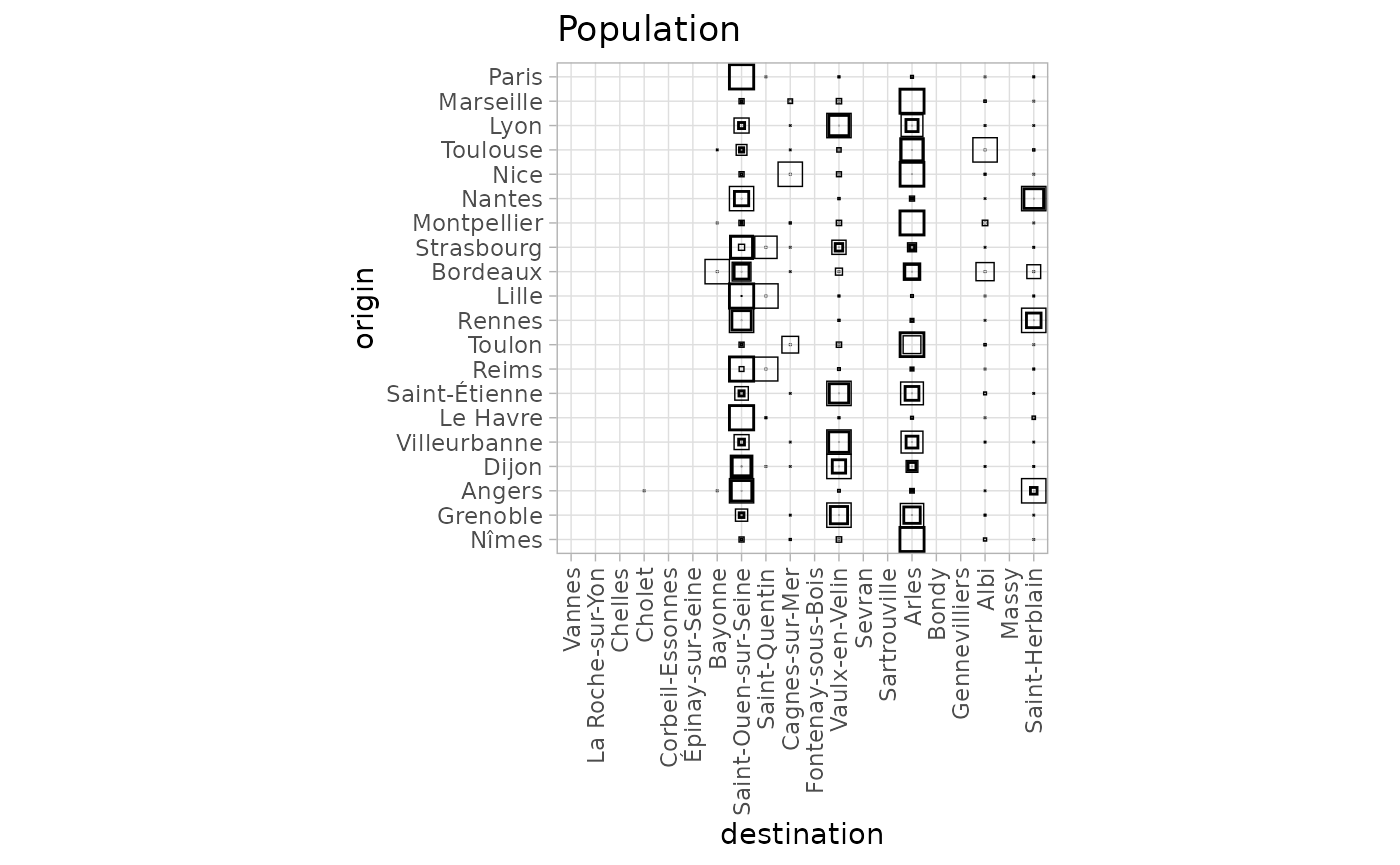

A variability plot matrix for flows from large cities (y-axis) to small cities (y-axis). Compared to the log population representation, it shows more empty columns as well as more spreaded flows. On particular, the full column of squares associated to Vaulx-en-Velin has been replaced by a more empty one, with large cities sending next to no flow to Vaulx-en-Velin (for instance Paris, Nantes, Lille, etc.). On the contrary Saint-Ouen-sur-Seine and Arles, show more full squares has they receive flow from more large cities.

This can also be seen on the destination flow variability plots, especially by comparing both graphical representations.

autoplot(fr_models, with_names = TRUE, flow = "destination") +
  labs(title = "Log population") +
  coord_flip()

A horizontal bar chart displaying flow statistics for the 20 small French cities. Vaulx-en-Velin dominates with a very long bar showing a median incoming flow larger than the maximum flow of all cites excepted Arles. Only 4 cities out of 20 have a non zero median incoming flow (Saint-Herblain, Arles, Vaulx-en-Velin and Saint-Quentin). 9 cities have a zero maximum incoming flow.

autoplot(fr_models_direct, with_names = TRUE, flow = "destination") +
  labs(title = "Population") +
  coord_flip()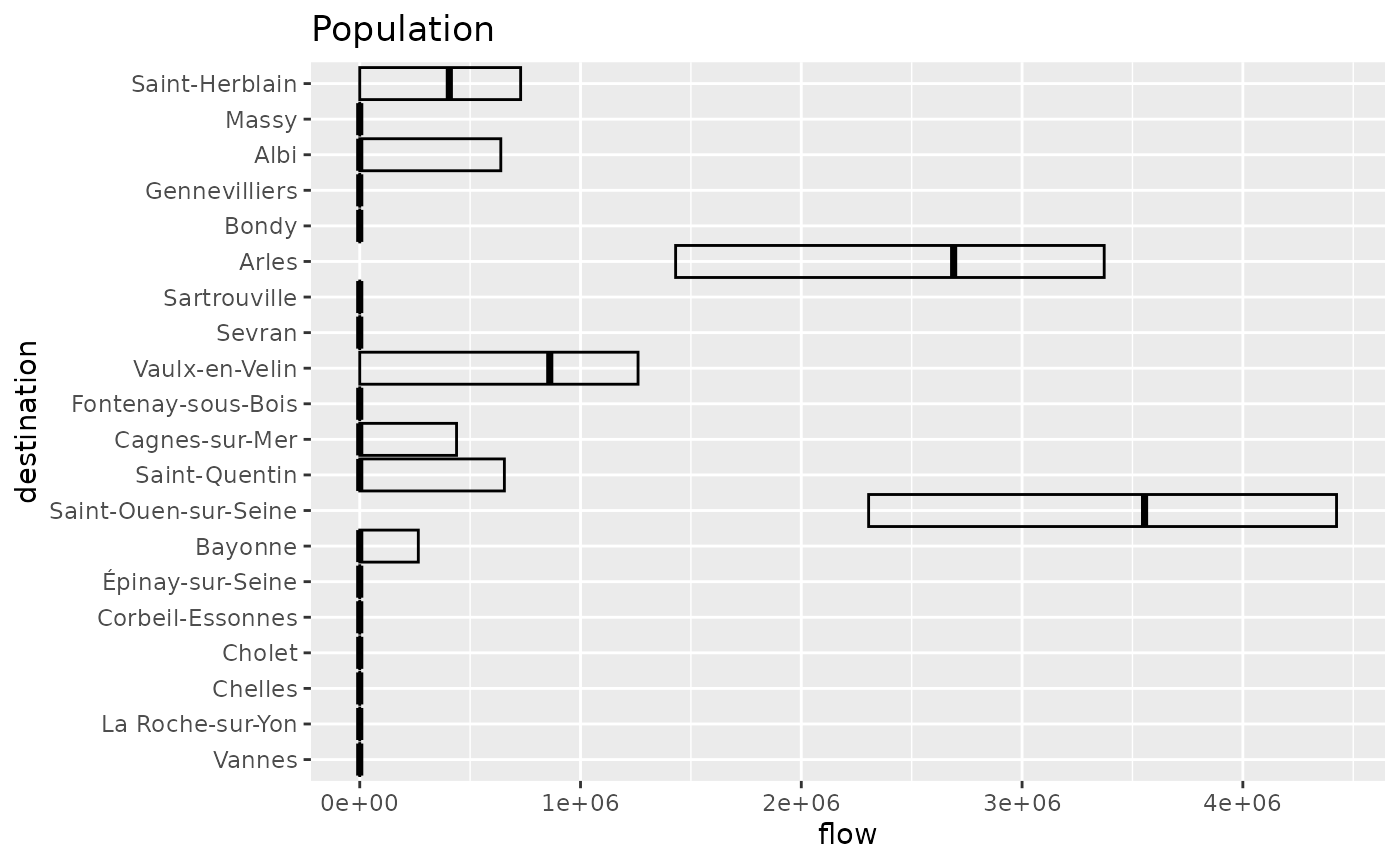

A horizontal bar chart displaying flow statistics for the 20 small French cities. Saint-Ouen-sur-Seine dominates with a very long bar showing a median incoming flow larger than the maximal incoming flow of all other cities. Only 4 cities have a non zero median incoming flow: Saint-Herblain, Arles Vaulx-en-Velin and Saint-Ouen-sur-Seine. 12 cities have a zero maximal incoming flow.

Finally, the geographical representation shows the emergence of these smaller cities.

options("ggrepel.max.overlaps" = 20)
autoplot(fr_models_direct,
  flows = "destination", with_names = TRUE,
  with_positions = TRUE
) +
  coord_sf(crs = "epsg:4326") +
  labs(title = "Population")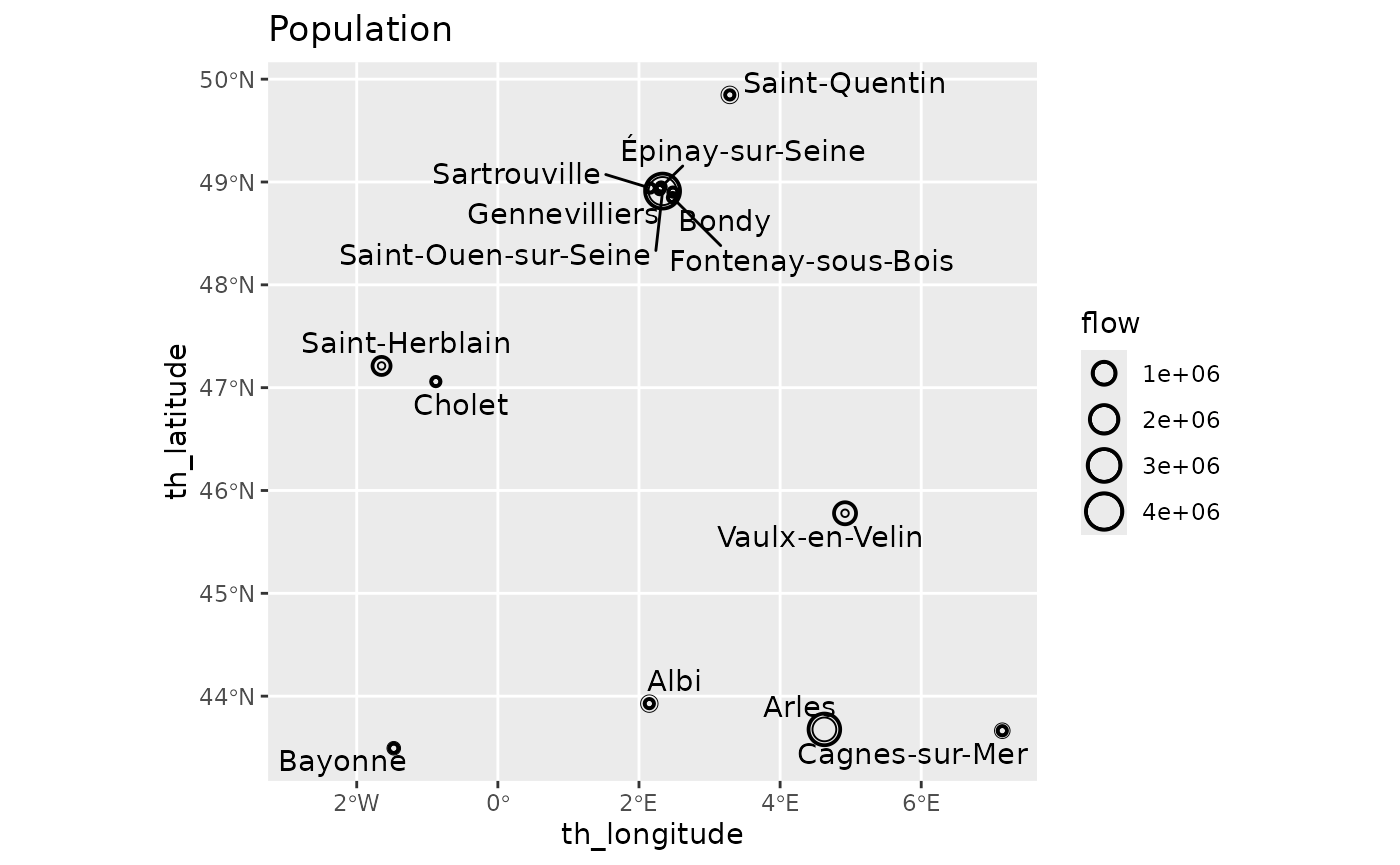

A geographic plot of France where flow statistics for the 20 destination cities are represented by circles of varying sizes and thicknesses. The cities receiving flows are spreaded over the set of destination cities. Compared to the log population case, the figure displays more active cities around Paris, a reduced influence of Vaulx-en-Velin and an increased influence of Arles.

By default, the flows are not normalised in the variability plot, and the global normalisation emphasises Paris’ dominance and its preferred destination, Saint-Ouen-sur-Seine, more strongly. This representation shows similar patterns for Marseille with Arles and to a lesser extent for Lyon with Vaulx-en-Velin, and Toulouse with Arles and Albi.

autoplot(fr_models_direct, with_names = TRUE, normalisation = "full") +
  theme_light() +
  theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust = 1)) +
  labs(title = "Population global normalisation")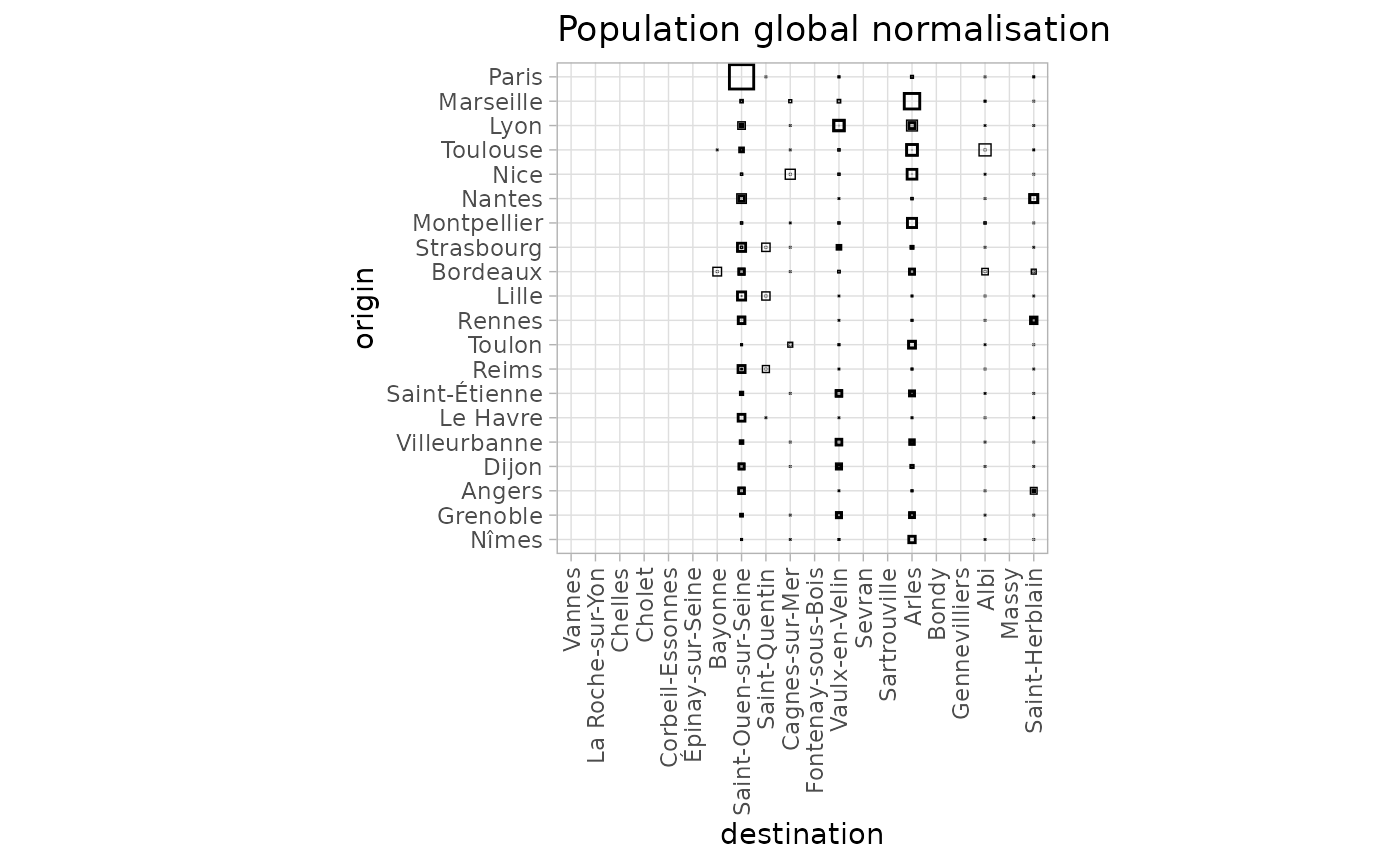

A variability plot matrix for flows from large cities (y-axis) to small cities (y-axis). Compared to the normalised representation, it shows far less big squares as the global flow is dominated by Paris, followed by Marseille, Lyon and Toulouse. This manifests by the presence of a lot of small squares together with largee on between Paris and Saint-Ouen-sur-Seine. There is also a relatively large square between Marseille and Arles, as well as medium ones between Lyon and Vaulx-en-Velin, and Toulouse and Arles.

Clustering

To investigate the differences between production constraints in more detail, we can cluster the results. As shown by the dendrograms and the cluster maps, the results are significantly influenced by the production constraints. As in the previous analyses, we use 16 clusters in a quite arbitrary way.

fr_models_dist <- sim_distance(fr_models, "destination")
fr_models_hc <- hclust(fr_models_dist, method = "ward.D2")
plot(fr_models_hc, hang = -1, labels = FALSE)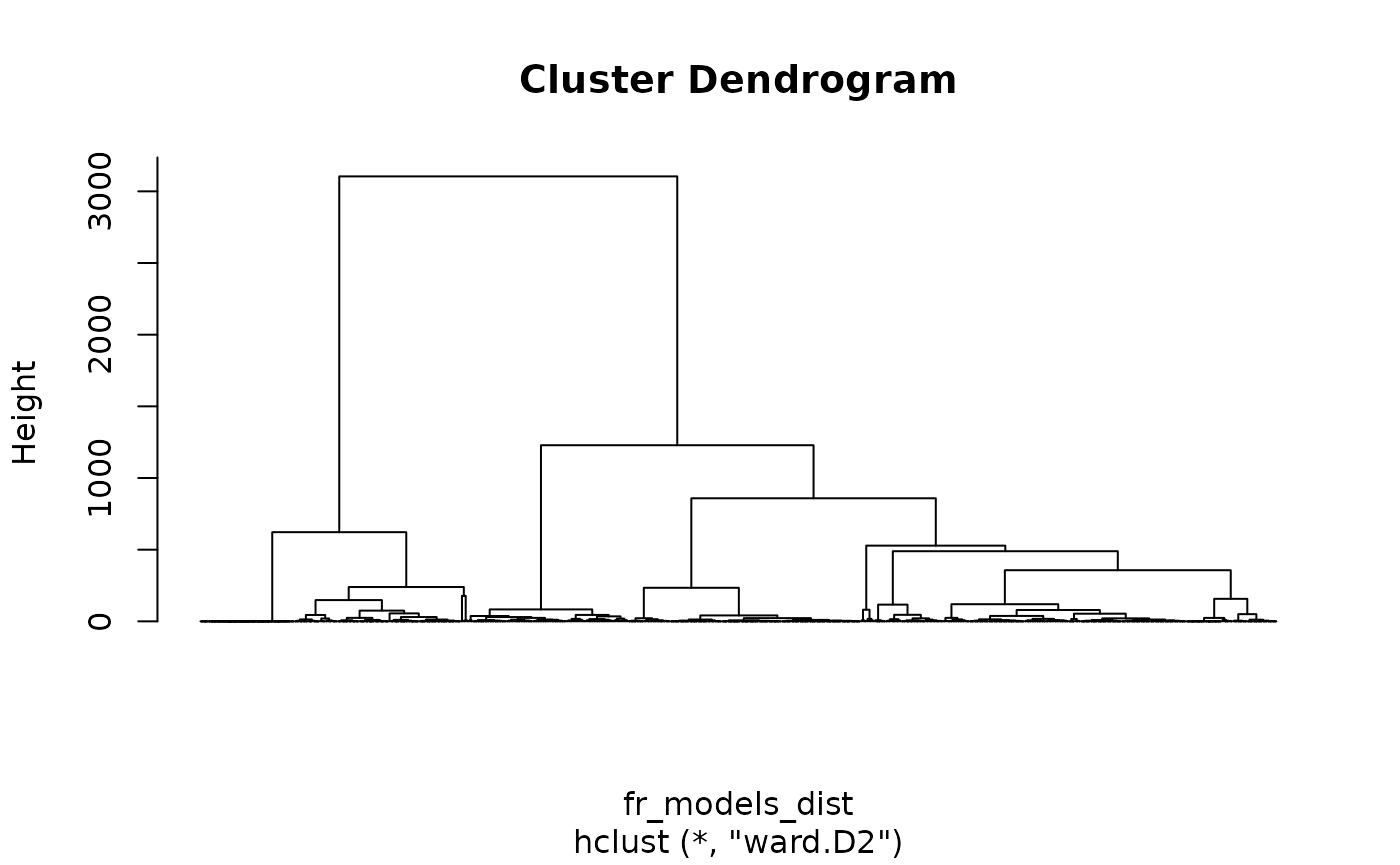

A Cluster Dendrogram for French city models using the ward.D2 method. The tree shows clear gaps in quality between 2, 3, 4 and 5 cluster solutions. The fifth cluster in this last case has a more complex structure than the other clusters, with a potential for being split into at least 3 sub-clusters.

fr_models_df$cluster <- as.factor(cutree(fr_models_hc, k = 16))
autoplot(fr_models_df, cluster) +
  theme(legend.position = "bottom") +
  guides(fill = guide_legend(nrow = 2)) +
  labs(title = "Log population")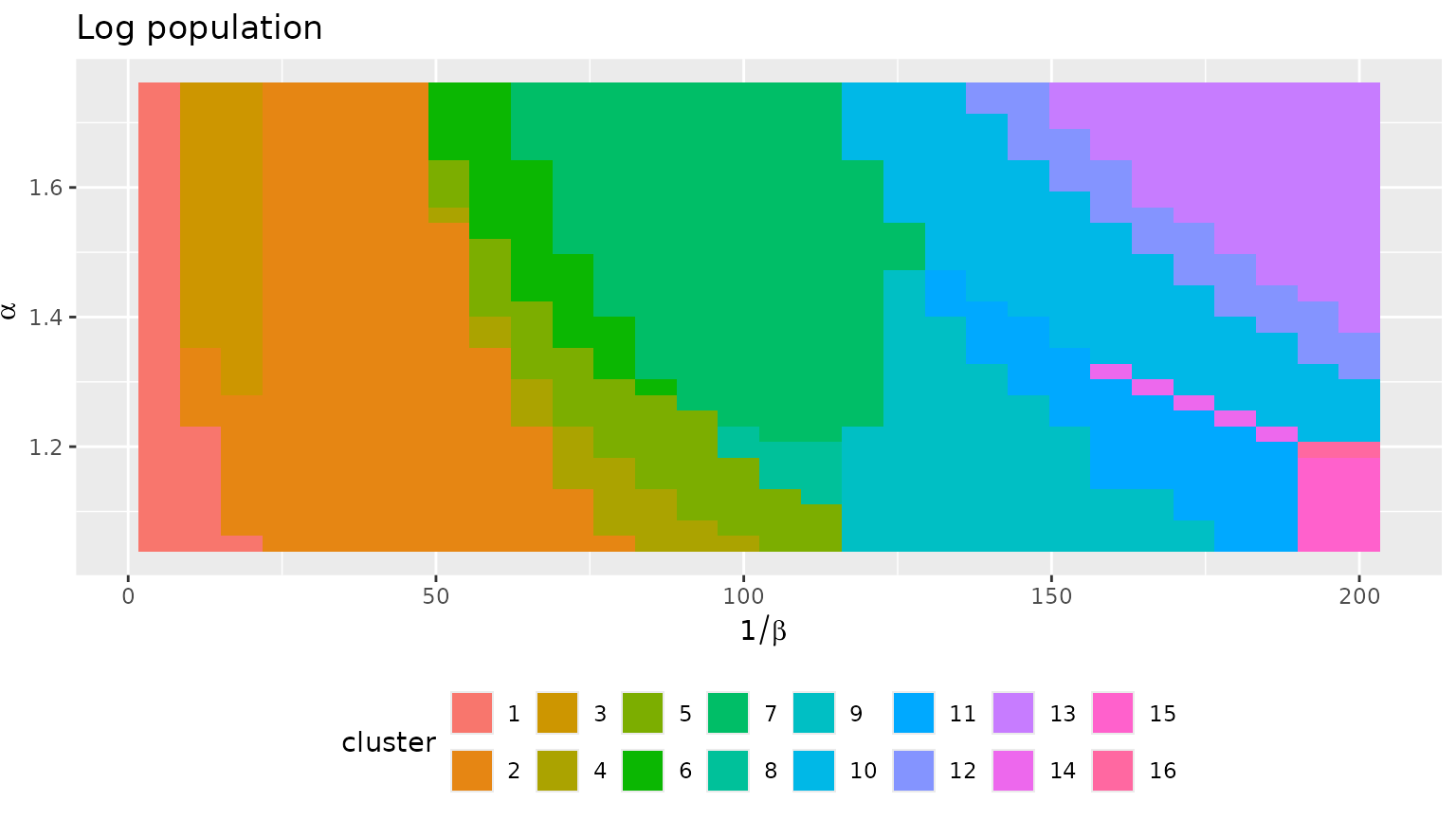

A heatmap showing the distribution of 16 clusters across a parameter space defined by alpha (y-axis) and 1/beta (x-axis) for European city models. The distribution is relatively complex (but spatially organised), showing that the chosen number of clusters is probably too high.

fr_models_direct_dist <- sim_distance(fr_models_direct, "destination")
fr_models_direct_hc <- hclust(fr_models_direct_dist, method = "ward.D2")
plot(fr_models_direct_hc, hang = -1, labels = FALSE)

A Cluster Dendrogram for French city models using the ward.D2 method. The tree is very different from the one obtained for the log population model. It shows two well balanced clusters. The left cluster can be split in a clear into 3 sub-clusters, while the right cluster has a clear sub-structure made of 2 sub-clusters that appear quite homogeneous.

fr_models_direct_df$cluster <- as.factor(cutree(fr_models_direct_hc, k = 16))
autoplot(fr_models_direct_df, cluster) +
  theme(legend.position = "bottom") +
  guides(fill = guide_legend(nrow = 2)) +
  labs(title = "Population")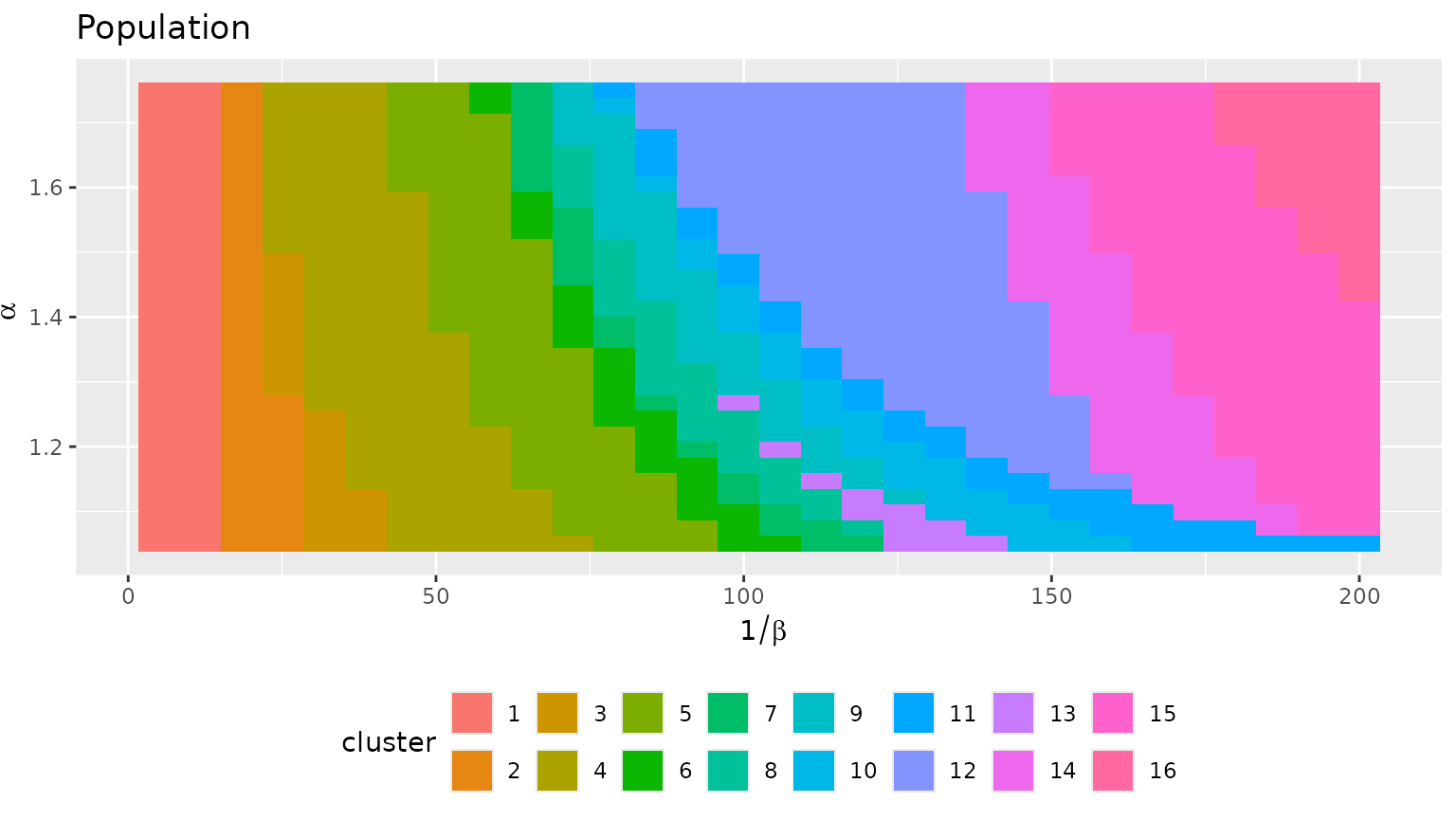

A heatmap showing the distribution of 16 clusters across a parameter space defined by alpha (y-axis) and 1/beta (x-axis) for European city models. The distribution is relatively complex (but spatially organised), showing that the chosen number of clusters is probably too high. Compared to the log population case, the clusters tend to be here more vertical, i.e. to correspond to bands of cost scale values spreaded over the full range of return to scale parameter. This may indicate that distances play here a stronger role than return to scale effects in shaping the flows.

The per-cluster variability plots are very informative. They show very limited variability within each cluster (as expected) and display different configurations. Contrast for instance cluster 13 for the log population model with cluster 16 for the direct population model. With the log population model, there are configurations with a single dominating site, cluster 13 (this aligns with the minimal value of the diversity which is r min(fr_models_df$diversity)). On the contrary, the direct population model does not lead to such as situation, we always have at least two important sites, as in cluster 16 (again, this aligns with the minimal value of the diversity, r round(min(fr_models_direct_df$diversity), 2)).

grid_var_autoplot(fr_models_df, cluster,
  flows = "destination",
  with_positions = TRUE
) +
  scale_size_continuous(range = c(0, 6)) +
  coord_sf(crs = "epsg:4326") +
  labs(title = "Log population")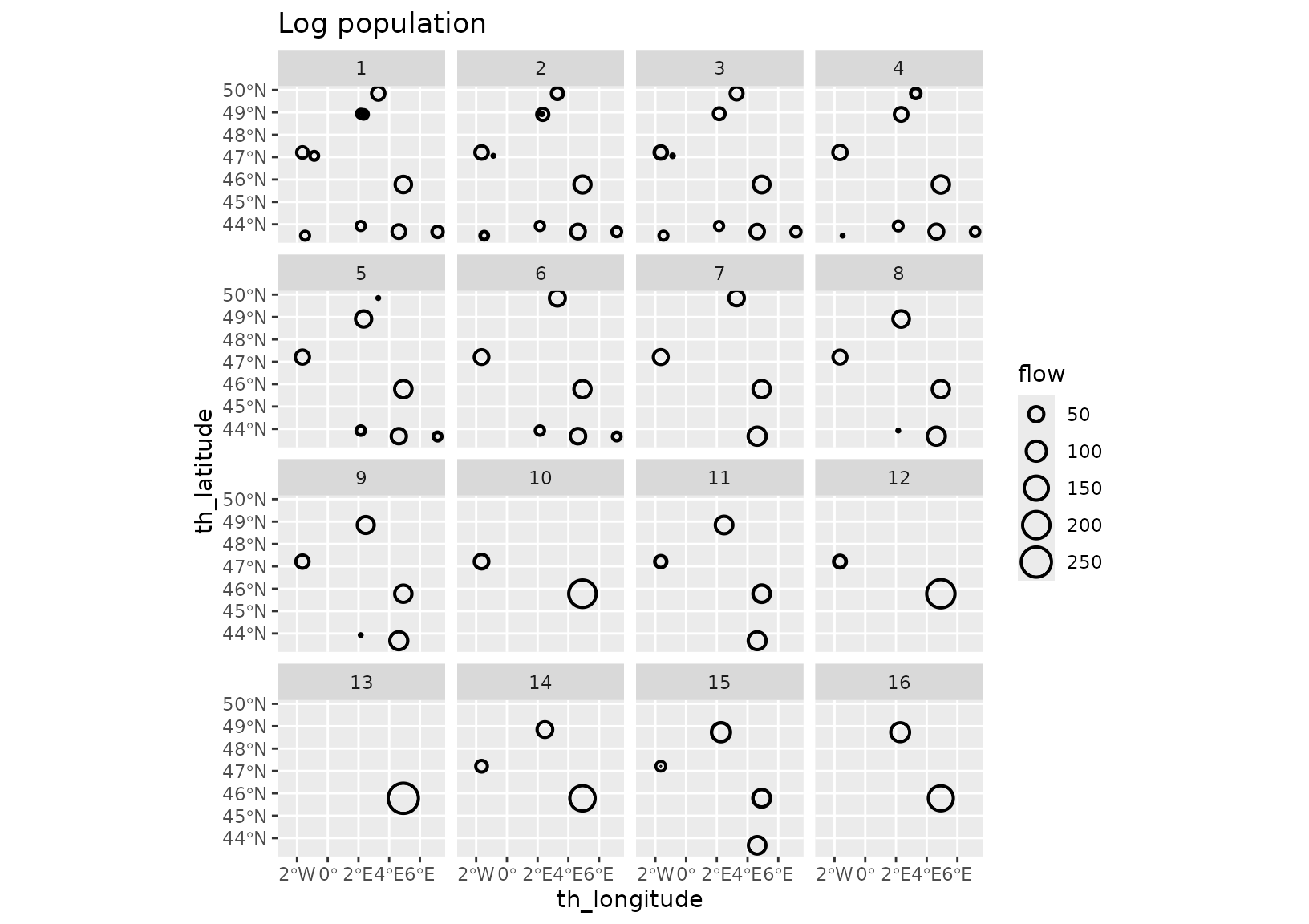

A 4x4 panel showing spatial flow circles for each of the 16 clusters of small french cities. Most of the circles have not inner or outer circles, showing a very strong homogeneity of the clusters. The flow distributions are varied from a single dominating destination in cluster 13 to 10 active cites in cluster 1. The reduction in the number of active cities consist first in removing reducing local redundancy (two close cities are replaced by a single one) and then reducing the flow to cities on the border of the map.

grid_var_autoplot(fr_models_direct_df, cluster,
  flows = "destination",
  with_positions = TRUE
) +
  scale_size_continuous(range = c(0, 6)) +
  coord_sf(crs = "epsg:4326") +
  labs(title = "Population")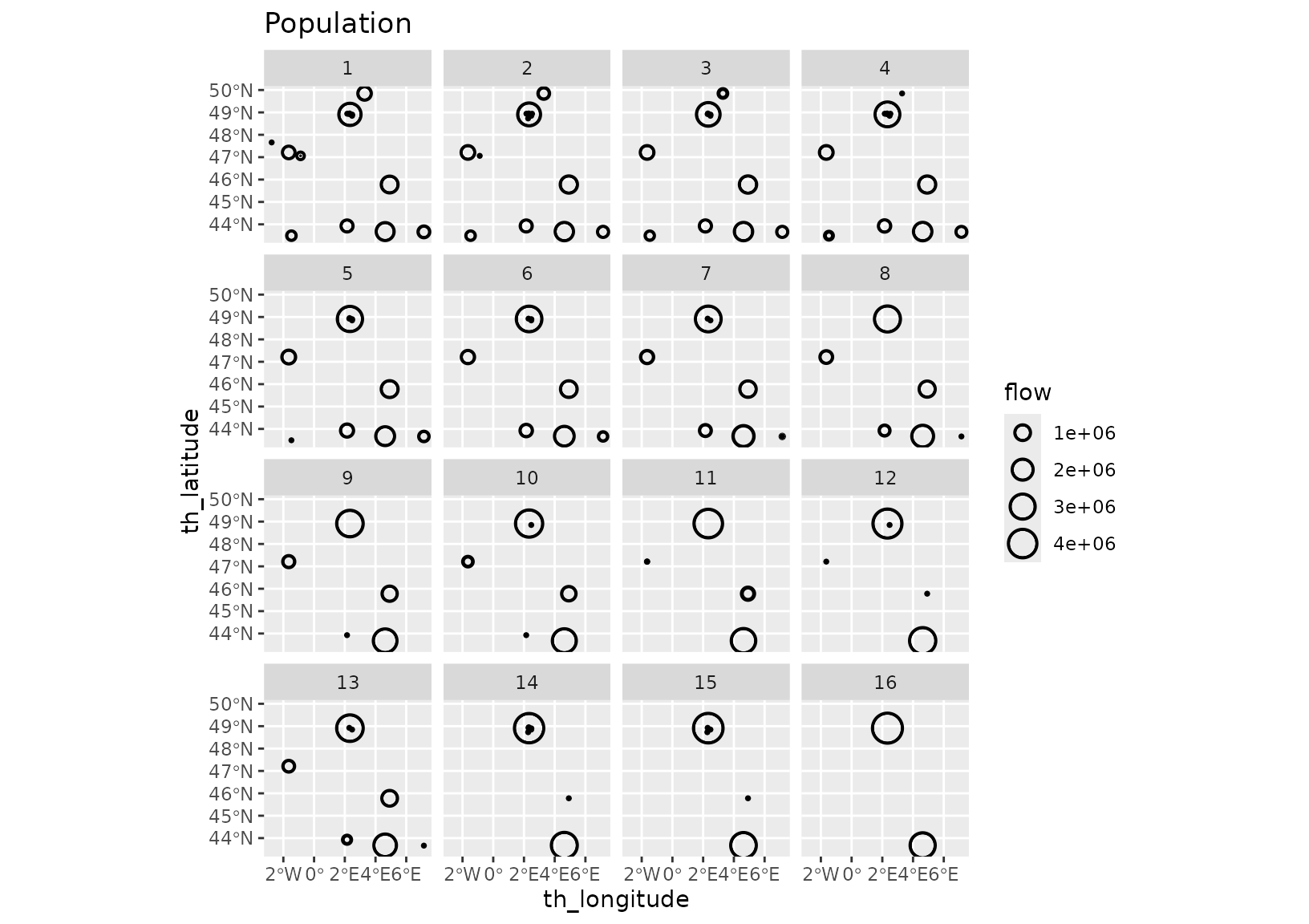

A 4x4 panel showing spatial flow circles for each of the 16 clusters of small french cities. Most of the circles have not inner or outer circles, showing a very strong homogeneity of the clusters. The flow distributions vary from a concentration on two cities (cluster 16) to situations with up to 12 active cities. A striking difference with the log population model is the presence of a collection of active cities near Paris despite the constant local (and global) domination of Saint-Ouen-sur-Seine whose circle is always the largest. One could prolong the analysis by investigating individual clusters, for instance by displaying the median models or a selection of diverse models.